Mathematical Structure & Dynamics of Aggregate System Dynamics Infectious Disease Models 2. Nathaniel Osgood CMPT 394 February 5, 2013
|
|
|
- Henry McCarthy
- 5 years ago
- Views:
Transcription
1 Mathematical Structure & Dynamics of Aggregate System Dynamics Infectious Disease Models 2 Nathaniel Osgood CMPT 394 February 5, 2013
2 Recall: Kendrick-McKermack Model Partitioning the population into 3 broad categories: Susceptible (S) Infectious (I) Removed (R)
3 Model Generality The model can be taken as describing many processes of contagion Transmission of computer malware Spread of word of mouth about a new product Rumor propagation Spread of a meme or idea
4 Recall: Basic Model Structure Population Size Immigration Rate Contacts per Susceptible Per Contact Risk of Infection Fractional Prevalence Average Duration of Infectiousness Immigration Susceptible Incidence Infective Recovery Recovered
5 State Equation Representation We can represent System Dynamics (stock & flow) models as state equations These are systems of first order differential equations Systems of arbitrary order can be represented in this way We can simply name the derive of a given state variable as another state variable
6 Recall: Mathematical Notation Immigration M Rate Per Contact Risk of Contacts per Infection Fractional Susceptible c Prevalence Population Size N Mean Time with Disease Immigration of Susceptibles Susceptible Incidence Absolute Prevalence S I R Recovery Recovered
7 Recall: Underlying Equations I S M c S N I I c S N I R I
8 Key Quantities for Infectious Disease Models: Parameters Contacts per susceptible per unit time: c e.g. 20 contacts per month This is the number of contacts a given susceptible will have with anyone Per-infective-with-susceptible-contact transmission probability: This is the per-contact likelihood that the pathogen will be transmitted from an infective to a susceptible with whom they come into a single contact.
9 Recall: Intuition Behind Common Terms I/N: The Fraction of population members (or, by assumption, contacts!) that are infective Important: Simplest models assume that this is also the fraction of a given susceptible s contacts that are infective! Many sophisticated models relax this assumption c(i/n): Average number of infectives that come into contact with a susceptible in a given unit time c(i/n) : Force of infection : (Approx.) likelihood a given susceptible will be infected per unit time The idea is that if a given susceptible comes into contact with c(i/n) infectives per unit time, and if each such contact gives likelihood of transmission of infection, then that susceptible has roughly a total likelihood of c(i/n) of getting infected per unit time (e.g. month)
10 Key Term: Rate of Infections Population Size Immigration Rate Contacts per Susceptible Per Contact Risk of Infection Fractional Prevalence Average Duration of Infectiousness Immigration Susceptible Incidence Infective Recovery Recovered
11 Key Term: Flow Rate of New Infections This is the key form of the equation in many infectious disease models Total # of susceptibles infected per unit time # of Susceptibles * Likelihood a given susceptible will be infected per unit time = S*( Force of Infection ) =S(c(I/N) ) Note that this is a term that multiplies both S and I! This non-linear term is much different than the purely linear terms on which we have previously focused Likelihood is actually a probability density (a value >1 indicates that mean time to infection is <1)
12 Another Useful View of Key Flow Recall: Total # of susceptibles infected per unit time = # of Susceptibles * Likelihood a given susceptible will be infected per unit time = S*( Force of Infection ) = S(c(I/N) ) The above can also be phrased as the following: S(c(I/N) )=I(c(S/N) )=I(c*f* )= # of Infectives * Mean # susceptibles infected per unit time by each infective This implies that as # of susceptibles falls=># of susceptibles surrounding each infective falls=>the rate of new infections falls ( Less fuel for the fire leads to a reduced burning rate)
13 A Critical Throttle on Infection Spread: Fraction Susceptible (f) The fraction susceptible (here, S/N) is a key quantity limiting the spread of infection in a population Recognizing its importance, we give this name f to the fraction of the population that is susceptible This fraction determines the efficiency of transmission from an infective
14 Infection Dynamics in a Closed Population (No Births, Deaths, Immigration)
15 Basic Model Structure Population Size Immigration Rate =0 Contacts per Susceptible Per Contact Risk of Infection Fractional Prevalence Average Duration of Infectiousness Immigration Susceptible Incidence Infective Recovery Recovered
16 Example Dynamics of SIR Model (No Births or Deaths) 2,000 people 600 people 10,000 people SIR Example 1,500 people 450 people 9,500 people 1,000 people 300 people 9,000 people 500 people 150 people 8,500 people 0 people 0 people 8,000 people Time (days) Susceptible Population S : SIR example Infectious Population I : SIR example Recovered Population R : SIR example people people people
17 Under what conditions does count of infectious individuals (I) decline? Answer: I declines iff (the following are equivalent) there is >1 infective and Outflow < Inflow: Rate at which people are recovering < Rate at which people are getting infected S(c(I/N) ) < I/ => S c /N < 1/ => (S/N c ) < 1 => A Person infects fewer than 1 person over the course of their illness
18 Example Dynamics of SIR Model (No Births or Deaths) 2,000 people 600 people 10,000 people SIR Example 1,500 people 450 people 9,500 people 1,000 people 300 people 9,000 people 500 people 150 people 8,500 people 0 people 0 people 8,000 people Time (days) Susceptible Population S : SIR example Infectious Population I : SIR example Recovered Population R : SIR example people people people
19 Explaining the Stock & Flow Dynamics: Infectives & Susceptibles Initially Each infective infects c(s/n) c people on average for each time unit the maximum possible rate The rate of recoveries is 0 In short term # Infectives grows (quickly)=> rate of infection rises quickly (Positive feedback!) Susceptibles starts to decline, but still high enough that each infective is surrounded overwhelmingly by susceptibles, so remains efficient at transmitting Over time, more infectives, and fewer Susceptibles Fewer S around each I =>Rate of infections per I declines Many infectives start recovering => slower rise to I Tipping point : # of infectives plateaus Aggregate Level: Rate of infections = Rate of recoveries Individual Level: Each infective infects exactly one replacement before recovering In longer term, declining # of infectives & susceptibles => Lower & lower rate of new infections! Change in I dominated by recoveries => goal seeking to 0 (negative feedback!)
20 Key Point Maximum value of stock of infectives occurs at different time than maximum of incidence! Maximum of incidence depends on both susceptible count and force of infection
21 Case 1: Outbreak 2,000 people 600 people 10,000 people 1,500 people 450 people 9,500 people + Contacts between Susceptibles and Infectives + + Susceptibles + Infectives - New Infections + - SIR Example 1,000 people 300 people 9,000 people 500 people 150 people 8,500 people 0 people 0 people 8,000 people + Contacts between Susceptibles and Infectives + + Susceptibles + Infectives New Recoveries New Infections New Recoveries + Contacts between Susceptibles and Infectives + + Susceptibles + Infectives New Recoveries Time (days) New Infections Susceptible Population S : SIR example Infectious Population I : SIR example Recovered Population R : SIR example people people people
22 Shifting Feedback Dominance 2,000 people 600 people 10,000 people 1,500 people 450 people 9,500 people + Contacts between Susceptibles and Infectives + + Susceptibles + Infectives - New Infections + - SIR Example 1,000 people 300 people 9,000 people 500 people 150 people 8,500 people 0 people 0 people 8,000 people + Contacts between Susceptibles and Infectives + + Susceptibles + Infectives New Recoveries New Infections New Recoveries + Contacts between Susceptibles and Infectives + + Susceptibles + Infectives New Recoveries Time (days) New Infections Susceptible Population S : SIR example Infectious Population I : SIR example Recovered Population R : SIR example people people people
23 What is the Maximum Count of Infectious Cases (Prevalent Case Count) I is not changing at this peak I I I c S N 0 I is non-zero here c S 0 c S 1 0 N N S 1 S I R c We will be giving this a name the basic Reproductive number
24 State Space (Phase Space) We commonly view dynamics as by watching a variable as a function of time, but this is just a single perspective State space ( Phase Space ) diagrams depict the state space (phase space) of a system This is a space defined by coordinates corresponding to each successive state variable At a given point in time, the system occupies a particular position in that space Over time, system defined by state equations will typically etch out a trajectory in state space Note that this trajectory is specific to a particular set of parameters
25 An Example Phase Space
26 State Space (Phase Space) Diagrams State space ( Phase Space ) diagrams depict subsets (possibly complete) of the state space (phase space) of a system This is a space defined by coordinates that gives the value One axis for each state variable Time is implicit: Just movement on a trajectory dx/dt vector field over coordinates x Shows how quickly is changing at different point Note that these figures are specific to a particular set of parameters
27 State Space Plot
28 Case 2: Infection declines immediately Infectives Time (Month) Infectives : Infection extinction
29 State Space Portrait of Similar Activity
30 Under What Conditions Does Each Situation ( Case ) Apply? Hint: Under what conditions does count of infectious individuals (I) decline? Answer: I declines if (the following are equivalent) Outflow < Inflow: Rate at which people are recovering < Rate at which people are getting infected S(c(I/N) ) < I/ => S c /N < 1/ => (S/N c ) < 1 => A Person infects fewer than 1 person over the course of their illness If I=1 (initial state) and population (N) is large, S/N 1, and we have c < 1 as criterion
31 Where are the Equilibria ( Fixed Points ) Hint: Under what situations is the model in stasis (in balance?) Hint 2: Under what conditions are the rates of change of the stocks 0? Solution: Solve for the values of the state variables (in terms of the parameters) at which the derivatives [left hand sides of state equations] equal 0) These will be the points in state space at which there is no change
32 Recall: Mathematical Notation Immigration M Rate Per Contact Risk of Contacts per Infection Fractional Susceptible c Prevalence Population Size N Mean Time with Disease Immigration of Susceptibles Susceptible Incidence Absolute Prevalence S I R Recovery Recovered
33 Recall: Underlying Equations I S M c S N I I c S N I R I
34 Recall: Underlying Equations I S 0 c S N I I c S N I R I
35 Recall: Underlying Equations I S 0 c S N I I c S N R N S I I
36 In Balance When I S 0 c S 0 N I I I c S N 0
37 In Balance When I c S N I I c S N I This implies that I = 0. This makes all other terms derivative 0 as well!
38 Equilibria For this model, any state with 0 infectives (i.e. where S+R=N) is an equilibrium Not all such states are stable Stability: Some states will exhibit resilience (robustness) in response to disturbance (e.g. entry of an infectious person) Instability: Other states are fragile in the sense that a changed condition will totally change the state We will examine how to determine the stability of a given fixed point in a future session
39 Infection Dynamics in an Open Population
40 Introducing Births & Deaths How and why would introduction of birth & death affect system behaviour (assume for now a fixed total population size i.e. births=deaths, and that babies are born susceptible)
41 Introducing Births & Deaths How and why would introduction of birth & death affect system behaviour (assume for now a fixed total population size i.e. births=deaths, and that babies are born susceptible) How would this change long term behavior? Under what condition would the stock of susceptibles be declining? Under what condition would the stock of infectives be declining?
42 Slides Adapted from External Source Redacted from Public PDF for Copyright Reasons
43 Blue: # Susceptible Red: # infective Green: Force of Infection This is the point where Rate of new infections=rate of recoveries A person infects on average 1 person before recovering The level of susceptibles is at the lowest level where the infection is sustainable (in the short run) At this point # susceptibles = # susceptibles at endemic equilibrium Why is the # of susceptibles rising, to well above its sustainable value? Why is the # of susceptibles still declining? This fraction of susceptibles at endemic equilibrium is the minimum sustainable value of susceptible i.e. the value where the properties above hold. Above this fraction of susceptibles, the # infected will rise
44 This is the point where Rate of new infections=rate of recoveries A person infects on average 1 person before recovering The level of susceptibles is at the lowest level where the infection is sustainable (in the short run) The rise is occurring because infectives are so low that so few infections occur that births >infections+deaths. S rises above the sustainable value because infectives are Still in decline until that point so infectives remain low For a while! The susceptibles are still declining here because the large # of infectives still causes enough infections that rate of immigration < rate of infections + deaths
45 Delays For a while after infectives start declining (i.e. susceptibles are below sustainable endemic value), they still deplete susceptibles sufficiently for susceptibles to decline For a while after susceptibles are rising (until susceptibles=endemic value), infectives will still decline For a while after infectives start rising, births > # of infections =>susceptibles will rise to a peak well above endemic level
46 Reminder: No Birth & Death
47 High Birth (& Death) Rate: 0.05
48 Modest Birth (& Death) Rate: 0.02
49 Modest Birth (& Death) Rate: 0.005
50 Small Birth (& Death) Rate: 0.001
51 Equilibria: How Many? Disease free No infectives in population Entire population is susceptible Endemic Steady-state equilibrium produced by spread of illness Assumption is often that children get exposed when young The stability of the these equilibria (whether the system departs from them when perturbed) depends on the parameter values For the disease-free equilibrium on R 0
52 Equilibrium Behaviour With Births & Deaths, the system can approach an endemic equilibrium where the infection stays circulating in the population but in balance The balance is such that (simultaneously) The rate (in people/unit time) of new infections = The rate of immigration Otherwise # of susceptibles would be changing! The rate of new infections = the rate of recovery Otherwise # of infectives would be changing! For simplicity, we assumed a fixed population, but similar properties will hold
53 Tipping Point Now try setting transmission rate β to 0.005
54 Case 2: Infection declines immediately Infectives Time (Month) Infectives : Infection extinction
55 Recall: Closed Population (No Birth & Death) Infection always dies out in the population Some infections will take longer to die out There is a tipping point between two cases # of people infected declines out immediately Infection causes an outbreak before the infection dies down (# of people infected rises and then falls)
56 Simple Model Incorporating Population Turnover Contacts per Susceptible Per Contact Risk of Infection <Fractional Prevalence> Mean Time with Disease Susceptible Incidence Susceptible Mortality <Mortality Rate> Infectives Recovery Infective Mortality <Mortality Rate> Recovered Recovered Mortality <Mortality Rate>
57 Our model Set c=10 (people/month) =0.04 (4% chance of transmission per S-I contact) μ=10 Birth and death rate=0.02 Initial infectives=1, other 1000 susceptible
58 Here, the Infection Can Remain (Endemic)
59 Damped Oscillatory Behavior Modify model to have births and deaths, with an annual birth-and-death rate Set Model/Settings/Final Time to 1000 (long time frame) In Synthesim ( Running man ) mode, set Birth/death rates
60 Exploring the Tipping Point Now try setting transmission rate β to 0.005
61 Infection Extinction As for the case with a closed population, an open population has two cases Infection dies out immediately Infectives Outbreak: Infection takes off Here in contrast to the case for a closed population the infection will typically go to an endemic equilibrium Time (Month) Infectives : Infection extinction
62 Slides Adapted from External Source Redacted from Public PDF for Copyright Reasons
63 Infection Recall: For this model, a given infective infects c(s/n) others per time unit This goes up as the number of susceptibles rises Questions If the mean time a person is infective is μ, how many people does that infective infect before recovering? With the same assumption, how many people would that infective infect if everyone else is susceptible? Under what conditions would there be more infections after their recovery than before?
64 Fundamental Quantities We have just discovered the values of 2 famous epidemiological quantities for our model Effective Reproductive Number: R * Basic Reproductive Number: R 0
65 Effective Reproductive Number: R * Number of individuals infected by an index infective (over the course of their illness) in the current epidemological context Depends on Contact frequency (people/unit time) Transmission probability Length of time infected # (Fraction) of Susceptibles Affects Whether infection spreads If R * > 1, # of cases will rise, If R * <1, # of cases will fall Alternative formulation: Largest real eigenvalue <> 0 Endemic Rate
66 Basic Reproduction Number: R 0 Number of individuals infected by an index infective in an otherwise disease-free equilibrium This is just R * at disease-free equilibrium all (other) people in the population are susceptible other than the index infective Depends on Contact frequency (people/unit time) Transmission probability Length of time infected Affects Whether infection spreads If R 0 > 1, Epidemic Takes off, If R 0 <1, Epidemic dies out Alternative formulation: Largest real eigenvalue <> 0 Speed of spread: Initial infection rise exp(t*(r 0-1)/D) Endemic Rate
67 Basic Reproductive Number R 0 If contact patterns & infection duration remain unchanged and if fraction f of the population is susceptible, then mean # of individuals infected by an infective over the course of their infection is f*r 0 In endemic equilibrium: Inflow=Outflow (S/N) R 0 =1 Every infective infects a replacement infective to keep equilibrium Just enough of the population is susceptible to allow this replacement The higher the R 0, the lower the fraction of susceptibles in equilibrium! Generally some susceptibles remain: At some point in epidemic, susceptibles will get so low that can t spread
68 Our model Set c=10 (people/month) =0.04 (4% chance of transmission per S-I contact) μ=10 Birth and death rate= 0 Initial infectives=1, other 1000 susceptible What is R 0? What should we expect to see?
69 Thresholds R * Too low # susceptibles => R* < 1: # of infectives declining Too high # susceptibles => R* > 1: # of infectives rising R 0 R 0 >1: Infection is introduced from outside will cause outbreak R 0 <1: Herd immunity : infection is introduced from outside will die out (may spread to small number before disappearing, but in unsustainable way) This is what we try to achieve by control programs, vaccination, etc. Outflow from susceptibles (infections) is determined by the # of Infectives
70 Equilibrium Behaviour With Births & Deaths, the system can approach an endemic equilibrium where the infection stays circulating in the population but in balance The balance is such that (simultaneously) The rate of new infections = The rate of immigration Otherwise # of susceptibles would be changing! The rate of new infections = the rate of recovery Otherwise # of infectives would be changing!
71 Equilibria Disease free No infectives in population Entire population is susceptible Endemic Steady-state equilibrium produced by spread of illness Assumption is often that children get exposed when young The stability of the these equilibria (whether the system departs from them when perturbed) depends on the parameter values For the disease-free equilibrium on R 0
72 Vaccination
73 Adding Vaccination Stock Add a Vaccinated stock A constant called Monthly Likelihood of Vaccination Vaccination flow between the Susceptible and Vaccinated stocks The rate is the stock times the constant above Set initial population to be divided between 2 stocks Susceptible Vaccinated Incorporate Vaccinated in population calculation
74 Additional Settings c= 10 Beta=.04 Duration of infection = 10 Birth & Death Rate=0
75 Adding Stock
76 Experiment with Different Initial Vaccinated Fractions Fractions = 0.25, 0.50, 0.6, 0.7, 0.8
77
78 Recall: Thresholds R* Too low # susceptibles => R* < 1: # of infectives declining Too high # susceptibles => R* > 1: # of infectives rising Outflow from susceptibles (infections) is determined by the # of Infectives Delays: For a while after infectives start declining, they still deplete susceptibles sufficiently for susceptibles to decline For a while after infectives start rising, the # of infections is insufficient for susceptibles to decline
79 Effective Reproductive Number: R * Number of individuals infected by an index infective in the current epidemiological context Depends on Contact number Transmission probability Length of time infected # (Fraction) of Susceptibles Affects Whether infection spreads If R * > 1, # of cases will rise, If R * <1, # of cases will fall Alternative formulation: Largest real eigenvalue <> 0 Endemic Rate
80 Basic Reproduction Number: R 0 Number of individuals infected by an index infective in an otherwise disease-free equilibrium This is just R * at disease-free equilibrium all (other) people in the population are susceptible other than the index infective Depends on Contact number Transmission probability Length of time infected Affects Whether infection spreads If R 0 > 1, Epidemic Takes off, If R 0 <1, Epidemic dies out Alternative formulation: Largest real eigenvalue <> 0 Initial infection rise exp(t*(r0-1)/d) Endemic Rate
81 Recall: A Critical Throttle on Infection Spread: Fraction Susceptible (f) The fraction susceptible (here, S/N) is a key quantity limiting the spread of infection in a population Recognizing its importance, we give this name f to the fraction of the population that issusceptible If contact patterns & infection duration remain unchanged and, then mean # of individuals infected by an infective over the course of their infection is f*r 0
82 Recall: Endemic Equilibrium Inflow=Outflow (S/N) R 0 =f R 0 =1 Every infective infects a replacement infective to keep equilibrium Just enough of the population is susceptible to allow this replacement The higher the R 0, the lower the fraction of susceptibles in equilibrium! Generally some susceptibles remain: At some point in epidemic, susceptibles will get so low that can t spread
83 Critical Immunization Threshold Consider an index infective arriving in a worst case scenario when noone else in the population is infective or recovered from the illness In this case, that infective is most efficient in spreading The goal of vaccination is keep the fraction susceptible low enough that infection cannot establish itself even in this worst case We do this by administering vaccines that makes a person (often temporarily) immune to infection We say that a population whose f is low enough that it is resistant to establishment of infection exhibits herd immunity
84 Critical Immunization Threshold Vaccination seeks to lower f such that f*r 0 <1 Worst case: Suppose we have a population that is divided into immunized (vaccinated) and susceptible Let q c be the critical fraction immunized to stop infection Then f=1-q c, f*r 0 <1 (1-q c )*R 0 <1 q c >1-(1/R 0 ) So if R 0 = 4 (as in our example), q c =0.75(i.e. 75% of population must be immunized just as we saw!)
85 Open/Closed Population Open Population Closed Population Case Does Epidemic Occur? Fraction infective R 0 >1 Yes Such that Infection rate=recovery rate Steady-state R 0 <1 No 0 1 Fraction susceptible 1/R 0 R 0 >1 Yes 0 <1 (often <<1) but >0 R 0 <1 No 0 1
86 Effects of An Open Population (different Parameters) Infective Approaches endemic level where R * =1 & rate of new infections = rate of recoveries Time (Month) nfective : Baseline 2% Annual Turnover Because no new influx of susceptibles ( fuel ), infectives in constant Decline. Approaches 0 (disease-free equilibrium) Infective : Baseline Closed Population
87 Effects of An Open Population Susceptible 1, Approaches endemic level where R * =1 & rate of arrivals (via birth&migration) = rate of new infections+deaths Approaches disease-free level where no infection is occurring Time (Month) usceptible : Baseline 2% Annual Turnover usceptible : Baseline Closed Population
88 Recovereds Recovered 1, Time (Month) ecovered : Baseline 2% Annual Turnover ecovered : Baseline Closed Population
89 Impact of Turnover The greater the turnover rate, the greater the fraction of susceptibles in the population => the greater the endemic rate of infection
90 Fraction of Susceptibles
91 Effective Reproductive Number
92 Prevalence
93 R*
94 Fraction Recovered
95 Adding Ongoing Vaccination Process
96 Infectious Disease Models 5 -- Vaccination CMPT 858 Nathaniel Osgood
97 Equilibrium Behaviour With Births & Deaths, the system can approach an endemic equilibrium where the infection stays circulating in the population but in balance The balance is such that (simultaneously) The rate of new infections = The rate of immigration Otherwise # of susceptibles would be changing! The rate of new infections = the rate of recovery Otherwise # of infectives would be changing!
98 Equilibria Disease free No infectives in population Entire population is susceptible Endemic Steady-state equilibrium produced by spread of illness Assumption is often that children get exposed when young The stability of the these equilibria (whether the system departs from them when perturbed) depends on the parameter values For the disease-free equilibrium on R 0
99 Adding Vaccination Stock Add a Vaccinated stock A constant called Monthly Likelihood of Vaccination Vaccination flow between the Susceptible and Vaccinated stocks The rate is the stock times the constant above Set initial population to be divided between 2 stocks Susceptible Vaccinated Incorporate Vaccinated in population calculation
100 Additional Settings c= 10 Beta=.04 Duration of infection = 10 Birth & Death Rate=0
101 Adding Stock
102 Experiment with Different Initial Vaccinated Fractions Fractions = 0.25, 0.50, 0.6, 0.7, 0.8
103
104 Critical Immunization Threshold Consider an index infective arriving in a worst case scenario when noone else in the population is infective or recovered from the illness In this case, that infective is most efficient in spreading The goal of vaccination is keep the fraction susceptible low enough that infection cannot establish itself even in this worst case We do this by administering vaccines that makes a person (often temporarily) immune to infection We say that a population whose f is low enough that it is resistant to establishment of infection exhibits herd immunity
105 Critical Immunization Threshold Vaccination seeks to lower f such that f*r 0 <1 Worst case: Suppose we have a population that is divided into immunized (vaccinated) and susceptible Let q c be the critical fraction immunized to stop infection Then f=1-q c, f*r 0 <1 (1-q c )*R 0 <1 q c >1-(1/R 0 ) So if R 0 = 4 (as in our example), q c =0.75(i.e. 75% of population must be immunized just as we saw!)
106 Simulating Introduction of Vaccination for a Childhood Infection in an Open Population c = 500 Beta = 0.05 Duration of infection =.25 Initial Fraction Vaccinated = 0 Monthly birth & death rate = 10% per year (focusing on children 0-10 years of age) Questions What is R 0? What level of susceptibles is required to sustain the infection What is the critical vaccination fraction?
107
108 What Rate of Vaccination Eliminates?
109
110 Representing Quarantine
111
112
113 Endemic Situations In an endemic context, infection remains circulating in the population The common assumption here is that The susceptible portion of the population will be children At some point in their life trajectory (at an average age of acquiring infection A), individuals will be exposed to the infection & develop immunity
114 Slides Adapted from External Source Redacted from Public PDF for Copyright Reasons
115 Age of Exposure & Reproductive Constant Cf a natural (non-immunized) constant size population where all die at same age and where Mean Age at death L Mean Age of exposure A (i.e. we assume those above A are exposed) Fraction susceptible is S/N = A/L (i.e. proportion of population below age A) Recall for our (and many but not all other) models: R*=(S/N)R 0 =1 S/N=1/R 0 Thus A/L = 1/R 0 L/A = R 0 This tells us that the larger the R 0, the earlier in life individuals become infected
116 Incompletely Immunized Population Suppose we have q fraction of population immunized (q<q c ) Suppose we have fraction f susceptible Fraction of the population currently or previously infected is 1-q-f If we assume (as previously) that everyone lives until L and is infected at age A, then fraction 1-A/L has been infected So 1-A/L= 1-q-f A = L(q+f) This can be much higher than for the natural population This higher age of infection can cause major problems, due to waning of childhood defenses i.e. incomplete immunization leads to older mean age ofexposure
117
Essentials of Aggregate System Dynamics Infectious Disease Models. Nathaniel Osgood CMPT 858 FEBRUARY 3, 2011
 Essentials of Aggregate System Dynamics Infectious Disease Models Nathaniel Osgood CMPT 858 FEBRUARY 3, 2011 Mathematical Models Link Together Diverse Factors Typical Factors Included Infection Mixing
Essentials of Aggregate System Dynamics Infectious Disease Models Nathaniel Osgood CMPT 858 FEBRUARY 3, 2011 Mathematical Models Link Together Diverse Factors Typical Factors Included Infection Mixing
Infectious Disease Models 3. Nathaniel Osgood CMPT 858 March 16, 2010
 Infectious Disease Models 3 Nathaniel Osgood CMPT 858 March 16, 2010 Key Quantities for Infectious Disease Models: Parameters Contacts per susceptible per unit time: c e.g. 20 contacts per month This is
Infectious Disease Models 3 Nathaniel Osgood CMPT 858 March 16, 2010 Key Quantities for Infectious Disease Models: Parameters Contacts per susceptible per unit time: c e.g. 20 contacts per month This is
Infectious Disease Models 4: Basic Quantities of Mathematical Infectious Disease Epidemiology. Nathaniel Osgood CMPT
 Infectious Disease Models 4: Basic Quantities of Mathematical Infectious Disease Epidemiology Nathaniel Osgood CMPT 858 3-18-2010 Recall: Closed Population (No Birth & Death) Infection always dies out
Infectious Disease Models 4: Basic Quantities of Mathematical Infectious Disease Epidemiology Nathaniel Osgood CMPT 858 3-18-2010 Recall: Closed Population (No Birth & Death) Infection always dies out
Essentials of Aggregate System Dynamics Infectious Disease Models
 Essentials of Aggregate System Dynamics Infectious Disease Models Nathaniel Osgood CMPT 394 February 5, 2013 Comments on Mathematics & Dynamic Modeling Many accomplished & well-published dynamic modelers
Essentials of Aggregate System Dynamics Infectious Disease Models Nathaniel Osgood CMPT 394 February 5, 2013 Comments on Mathematics & Dynamic Modeling Many accomplished & well-published dynamic modelers
Stocks & Flows 2: First Order Delays & Aging Chains
 Stocks & Flows 2: First Order Delays & Aging Chains Nathaniel Osgood CMPT 858 FEBRUARY 1, 2011 Example Model: Stocks Example Model: Flows Key Component: Stock & Flow Flow + Stock Flow Stock Structure &
Stocks & Flows 2: First Order Delays & Aging Chains Nathaniel Osgood CMPT 858 FEBRUARY 1, 2011 Example Model: Stocks Example Model: Flows Key Component: Stock & Flow Flow + Stock Flow Stock Structure &
L2, Important properties of epidemics and endemic situations
 L2, Important properties of epidemics and endemic situations July, 2016 The basic reproduction number Recall: R 0 = expected number individuals a typical infected person infects when everyone is susceptible
L2, Important properties of epidemics and endemic situations July, 2016 The basic reproduction number Recall: R 0 = expected number individuals a typical infected person infects when everyone is susceptible
MODELING DISEASE FINAL REPORT 5/21/2010 SARAH DEL CIELLO, JAKE CLEMENTI, AND NAILAH HART
 MODELING DISEASE FINAL REPORT 5/21/2010 SARAH DEL CIELLO, JAKE CLEMENTI, AND NAILAH HART ABSTRACT This paper models the progression of a disease through a set population using differential equations. Two
MODELING DISEASE FINAL REPORT 5/21/2010 SARAH DEL CIELLO, JAKE CLEMENTI, AND NAILAH HART ABSTRACT This paper models the progression of a disease through a set population using differential equations. Two
How Math (and Vaccines) Keep You Safe From the Flu
 How Math (and Vaccines) Keep You Safe From the Flu Simple math shows how widespread vaccination can disrupt the exponential spread of disease and prevent epidemics. By Patrick Honner BIG MOUTH for Quanta
How Math (and Vaccines) Keep You Safe From the Flu Simple math shows how widespread vaccination can disrupt the exponential spread of disease and prevent epidemics. By Patrick Honner BIG MOUTH for Quanta
The mathematics of diseases
 1997 2004, Millennium Mathematics Project, University of Cambridge. Permission is granted to print and copy this page on paper for non commercial use. For other uses, including electronic redistribution,
1997 2004, Millennium Mathematics Project, University of Cambridge. Permission is granted to print and copy this page on paper for non commercial use. For other uses, including electronic redistribution,
The effect of infectiousness, duration of sickness, and chance of recovery on a population: a simulation study
 Research Article The effect of infectiousness, duration of sickness, and chance of recovery on a population: a simulation study McKayla Johnson, Tashauna Gilliam, and Istvan Karsai East Tennessee State
Research Article The effect of infectiousness, duration of sickness, and chance of recovery on a population: a simulation study McKayla Johnson, Tashauna Gilliam, and Istvan Karsai East Tennessee State
Network Science: Principles and Applications
 Network Science: Principles and Applications CS 695 - Fall 2016 Amarda Shehu,Fei Li [amarda, lifei](at)gmu.edu Department of Computer Science George Mason University Spreading Phenomena: Epidemic Modeling
Network Science: Principles and Applications CS 695 - Fall 2016 Amarda Shehu,Fei Li [amarda, lifei](at)gmu.edu Department of Computer Science George Mason University Spreading Phenomena: Epidemic Modeling
Case Studies in Ecology and Evolution. 10 The population biology of infectious disease
 10 The population biology of infectious disease In 1918 and 1919 a pandemic strain of influenza swept around the globe. It is estimated that 500 million people became infected with this strain of the flu
10 The population biology of infectious disease In 1918 and 1919 a pandemic strain of influenza swept around the globe. It is estimated that 500 million people became infected with this strain of the flu
Sensitivity analysis for parameters important. for smallpox transmission
 Sensitivity analysis for parameters important for smallpox transmission Group Members: Michael A. Jardini, Xiaosi Ma and Marvin O Ketch Abstract In order to determine the relative importance of model parameters
Sensitivity analysis for parameters important for smallpox transmission Group Members: Michael A. Jardini, Xiaosi Ma and Marvin O Ketch Abstract In order to determine the relative importance of model parameters
Introduction to Stocks & Flows
 Introduction to Stocks & Flows Nathaniel Osgood (osgood@cs.usask.ca) CMPT 858 State of the System: Stocks ( Levels, State Variables, Compartments ) Stocks (Levels) represent accumulations These capture
Introduction to Stocks & Flows Nathaniel Osgood (osgood@cs.usask.ca) CMPT 858 State of the System: Stocks ( Levels, State Variables, Compartments ) Stocks (Levels) represent accumulations These capture
Mathematical Model of Vaccine Noncompliance
 Valparaiso University ValpoScholar Mathematics and Statistics Faculty Publications Department of Mathematics and Statistics 8-2016 Mathematical Model of Vaccine Noncompliance Alex Capaldi Valparaiso University
Valparaiso University ValpoScholar Mathematics and Statistics Faculty Publications Department of Mathematics and Statistics 8-2016 Mathematical Model of Vaccine Noncompliance Alex Capaldi Valparaiso University
The Epidemic Model 1. Problem 1a: The Basic Model
 The Epidemic Model 1 A set of lessons called "Plagues and People," designed by John Heinbokel, scientist, and Jeff Potash, historian, both at The Center for System Dynamics at the Vermont Commons School,
The Epidemic Model 1 A set of lessons called "Plagues and People," designed by John Heinbokel, scientist, and Jeff Potash, historian, both at The Center for System Dynamics at the Vermont Commons School,
Dynamics and Control of Infectious Diseases
 Dynamics and Control of Infectious Diseases Alexander Glaser WWS556d Princeton University April 9, 2007 Revision 3 1 Definitions Infectious Disease Disease caused by invasion of the body by an agent About
Dynamics and Control of Infectious Diseases Alexander Glaser WWS556d Princeton University April 9, 2007 Revision 3 1 Definitions Infectious Disease Disease caused by invasion of the body by an agent About
SARS Outbreak Study 2
 This week in Epiville, you will continue with the remaining steps of the outbreak investigation and begin to learn how to frame a hypothesis, design a study, and draw conclusions from your investigation.
This week in Epiville, you will continue with the remaining steps of the outbreak investigation and begin to learn how to frame a hypothesis, design a study, and draw conclusions from your investigation.
Step 1: Learning Objectives
 SARS Outbreak Study 2 This week in Epiville, you will continue with the remaining steps of the outbreak investigation and begin to learn how to frame a hypothesis, design a study, and draw conclusions
SARS Outbreak Study 2 This week in Epiville, you will continue with the remaining steps of the outbreak investigation and begin to learn how to frame a hypothesis, design a study, and draw conclusions
Mathematical Modeling of Infectious Disease
 Mathematical Modeling of Infectious Disease DAIDD 2013 Travis C. Porco FI Proctor Foundation for Research in Ophthalmology UCSF Scope and role of modeling In the most general sense, we may consider modeling
Mathematical Modeling of Infectious Disease DAIDD 2013 Travis C. Porco FI Proctor Foundation for Research in Ophthalmology UCSF Scope and role of modeling In the most general sense, we may consider modeling
Module 5: Introduction to Stochastic Epidemic Models with Inference
 Module 5: Introduction to Stochastic Epidemic Models with Inference Instructors:, Dept. Mathematics, Stockholm University Ira Longini, Dept. Biostatistics, University of Florida Jonathan Sugimoto, Vaccine
Module 5: Introduction to Stochastic Epidemic Models with Inference Instructors:, Dept. Mathematics, Stockholm University Ira Longini, Dept. Biostatistics, University of Florida Jonathan Sugimoto, Vaccine
Parasitism. Key concepts. Tasmanian devil facial tumor disease. Immunizing and non-immunizing pathogens. SI, SIS, and SIR epidemics
 Parasitism Key concepts Immunizing and non-immunizing pathogens SI, SIS, and SIR epidemics Basic reproduction number, R 0 Tasmanian devil facial tumor disease The Tasmanian devil Sarcophilus harrisii is
Parasitism Key concepts Immunizing and non-immunizing pathogens SI, SIS, and SIR epidemics Basic reproduction number, R 0 Tasmanian devil facial tumor disease The Tasmanian devil Sarcophilus harrisii is
Mathematical Model Approach To HIV/AIDS Transmission From Mother To Child
 Mathematical Model Approach To HIV/AIDS Transmission From Mother To Child Basavarajaiah.D. M. B. Narasimhamurthy, K. Maheshappa. B. Leelavathy ABSTRACT:- AIDS is a devastating disease, more than 2.50 million
Mathematical Model Approach To HIV/AIDS Transmission From Mother To Child Basavarajaiah.D. M. B. Narasimhamurthy, K. Maheshappa. B. Leelavathy ABSTRACT:- AIDS is a devastating disease, more than 2.50 million
Incidence functions and population thresholds. Density-dependent transmission. The incidence rate. Frequency-dependent transmission SI N SI N SI N
 ncidence functions and population thresholds Jamie Lloyd-mith Center for nfectious Disease Dynamics Pennsylvania tate University Outline ncidence functions Density dependence Population thresholds - nvasion
ncidence functions and population thresholds Jamie Lloyd-mith Center for nfectious Disease Dynamics Pennsylvania tate University Outline ncidence functions Density dependence Population thresholds - nvasion
Modelling the spread of HIV/AIDS epidemic in the presence of irresponsible infectives
 African Journal of Biotechnology Vol. (5, pp. 87-95, 6 June, Available online at http://www.academicjournals.org/ajb DOI:.5897/AJB.786 ISSN 684-535 Academic Journals Full Length Research Paper Modelling
African Journal of Biotechnology Vol. (5, pp. 87-95, 6 June, Available online at http://www.academicjournals.org/ajb DOI:.5897/AJB.786 ISSN 684-535 Academic Journals Full Length Research Paper Modelling
Module 5: Introduction to Stochastic Epidemic Models with Inference
 Module 5: Introduction to Stochastic Epidemic Models with Inference Instructors: Tom Britton, Dept. Mathematics, Stockholm University Ira Longini, Dept. Biostatistics, University of Florida Jonathan Sugimoto,
Module 5: Introduction to Stochastic Epidemic Models with Inference Instructors: Tom Britton, Dept. Mathematics, Stockholm University Ira Longini, Dept. Biostatistics, University of Florida Jonathan Sugimoto,
MMCS Turkey Flu Pandemic Project
 MMCS Turkey Flu Pandemic Project This is a group project with 2 people per group. You can chose your own partner subject to the constraint that you must not work with the same person as in the banking
MMCS Turkey Flu Pandemic Project This is a group project with 2 people per group. You can chose your own partner subject to the constraint that you must not work with the same person as in the banking
Generation times in epidemic models
 Generation times in epidemic models Gianpaolo Scalia Tomba Dept Mathematics, Univ of Rome "Tor Vergata", Italy in collaboration with Åke Svensson, Dept Mathematics, Stockholm University, Sweden Tommi Asikainen
Generation times in epidemic models Gianpaolo Scalia Tomba Dept Mathematics, Univ of Rome "Tor Vergata", Italy in collaboration with Åke Svensson, Dept Mathematics, Stockholm University, Sweden Tommi Asikainen
Epidemiological Model of HIV/AIDS with Demographic Consequences
 Advances in Applied Mathematical Biosciences. ISSN 2248-9983 Volume 5, Number 1 (2014), pp. 65-74 International Research Publication House http://www.irphouse.com Epidemiological Model of HIV/AIDS with
Advances in Applied Mathematical Biosciences. ISSN 2248-9983 Volume 5, Number 1 (2014), pp. 65-74 International Research Publication House http://www.irphouse.com Epidemiological Model of HIV/AIDS with
MODELLING THE SPREAD OF PNEUMONIA IN THE PHILIPPINES USING SUSCEPTIBLE-INFECTED-RECOVERED (SIR) MODEL WITH DEMOGRAPHIC CHANGES
 MODELLING THE SPREAD OF PNEUMONIA IN THE PHILIPPINES USING SUSCEPTIBLE-INFECTED-RECOVERED (SIR) MODEL WITH DEMOGRAPHIC CHANGES Bill William M. Soliman 1, Aldous Cesar F. Bueno 2 1, 2 Philippine Science
MODELLING THE SPREAD OF PNEUMONIA IN THE PHILIPPINES USING SUSCEPTIBLE-INFECTED-RECOVERED (SIR) MODEL WITH DEMOGRAPHIC CHANGES Bill William M. Soliman 1, Aldous Cesar F. Bueno 2 1, 2 Philippine Science
MATHEMATICAL STUDY OF BITING RATES OF MOSQUITOES IN TRANSMISSION OF DENGUE DISEASE
 ORIGINAL RESEARCH ARTICLE OPEN ACCESS MATHEMATICAL STUDY OF BITING RATES OF MOSQUITOES IN TRANSMISSION OF DENGUE DISEASE *G. R. Phaijoo, D. B. Gurung Department of Natural Sciences (Mathematics), School
ORIGINAL RESEARCH ARTICLE OPEN ACCESS MATHEMATICAL STUDY OF BITING RATES OF MOSQUITOES IN TRANSMISSION OF DENGUE DISEASE *G. R. Phaijoo, D. B. Gurung Department of Natural Sciences (Mathematics), School
Tuberculosis Tutorials
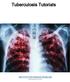 Tuberculosis Tutorials These tuberculosis (TB) tutorials were created for the EMOD QuickStart v1.8. Later versions of the QuickStart may not be completely compatible with these tutorials as installation
Tuberculosis Tutorials These tuberculosis (TB) tutorials were created for the EMOD QuickStart v1.8. Later versions of the QuickStart may not be completely compatible with these tutorials as installation
MAE 298, Lecture 10 May 4, Percolation and Epidemiology on Networks
 MAE 298, Lecture 10 May 4, 2006 Percolation and Epidemiology on Networks Processes on networks Search for information Spreading processes Interplay of topology and function Epidemiology Understanding how
MAE 298, Lecture 10 May 4, 2006 Percolation and Epidemiology on Networks Processes on networks Search for information Spreading processes Interplay of topology and function Epidemiology Understanding how
Heroin Epidemic Models
 Heroin Epidemic Models icholas A. Battista Intro to Math Biology Project School of Mathematical Sciences, Rochester Institute of Technology, 85 Lomb Memorial Drive, Rochester, Y 14623-5603, USA May 21,
Heroin Epidemic Models icholas A. Battista Intro to Math Biology Project School of Mathematical Sciences, Rochester Institute of Technology, 85 Lomb Memorial Drive, Rochester, Y 14623-5603, USA May 21,
Mathematical Modeling of Treatment SIR Model with Respect to Variable Contact Rate
 International Proceedings of Economics Development and Research IPEDR vol.83 (25) (25) IACSIT Press, Singapore Mathematical Modeling of Treatment SIR Model with Respect to Variable Contact Rate Paritosh
International Proceedings of Economics Development and Research IPEDR vol.83 (25) (25) IACSIT Press, Singapore Mathematical Modeling of Treatment SIR Model with Respect to Variable Contact Rate Paritosh
Adults and Children estimated to be living with HIV, 2013
 Adults and Children estimated to be living with HIV, 2013 Spending on HIV/AIDS Recent increase in the available money for HIV/AIDS The Gates foundation alone has over $60 billion Present plans are to hold
Adults and Children estimated to be living with HIV, 2013 Spending on HIV/AIDS Recent increase in the available money for HIV/AIDS The Gates foundation alone has over $60 billion Present plans are to hold
Global Stability of SACR Epidemic Model for Hepatitis C on Injecting Drug Users
 PROCEEDING OF 3 RD INTERNATIONAL CONFERENCE ON RESEARCH, IMPLEMENTATION AND EDUCATION OF MATHEMATICS AND SCIENCE YOGYAKARTA, 16 17 MAY 2016 Global Stability of SACR Epidemic Model for Hepatitis C on Injecting
PROCEEDING OF 3 RD INTERNATIONAL CONFERENCE ON RESEARCH, IMPLEMENTATION AND EDUCATION OF MATHEMATICS AND SCIENCE YOGYAKARTA, 16 17 MAY 2016 Global Stability of SACR Epidemic Model for Hepatitis C on Injecting
A Mathematical Approach to Characterize the Transmission Dynamics of the Varicella-Zoster Virus
 Proceedings of The National Conference On Undergraduate Research (NCUR) 2012 Weber State University, Ogden Utah March 29 31, 2012 A Mathematical Approach to Characterize the Transmission Dynamics of the
Proceedings of The National Conference On Undergraduate Research (NCUR) 2012 Weber State University, Ogden Utah March 29 31, 2012 A Mathematical Approach to Characterize the Transmission Dynamics of the
Disease dynamics: understanding the spread of diseases
 Disease dynamics: understanding the spread of diseases Image courtesy of Lightspring / shutterstock.com Get to grips with the spread of infectious diseases with these classroom activities highlighting
Disease dynamics: understanding the spread of diseases Image courtesy of Lightspring / shutterstock.com Get to grips with the spread of infectious diseases with these classroom activities highlighting
= Λ μs βs I N, (1) (μ + d + r)i, (2)
 Advanced Studies in Biology, Vol., 29, no. 8, 383-39 Mathematical Model of the Influenza A(HN) Infection K. Hattaf and N. Yousfi 2 Laboratory Analysis, Modeling and Simulation Department of Mathematics
Advanced Studies in Biology, Vol., 29, no. 8, 383-39 Mathematical Model of the Influenza A(HN) Infection K. Hattaf and N. Yousfi 2 Laboratory Analysis, Modeling and Simulation Department of Mathematics
Exercises on SIR Epidemic Modelling
 Exercises on SIR Epidemic Modelling 1 Epidemic model (from Wikipedia) An epidemic model is a simplified means of describing the transmission of communicable disease through individuals. The modeling of
Exercises on SIR Epidemic Modelling 1 Epidemic model (from Wikipedia) An epidemic model is a simplified means of describing the transmission of communicable disease through individuals. The modeling of
Mathematical Model of Hepatitis B in. the Bosomtwe District of Ashanti Region, Ghana
 Applied Mathematical Sciences, Vol. 8, 2014, no. 67, 3343-3358 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.44263 Mathematical Model of Hepatitis B in the Bosomtwe District of Ashanti
Applied Mathematical Sciences, Vol. 8, 2014, no. 67, 3343-3358 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.44263 Mathematical Model of Hepatitis B in the Bosomtwe District of Ashanti
Contents. Mathematical Epidemiology 1 F. Brauer, P. van den Driessche and J. Wu, editors. Part I Introduction and General Framework
 Mathematical Epidemiology 1 F. Brauer, P. van den Driessche and J. Wu, editors Part I Introduction and General Framework 1 A Light Introduction to Modelling Recurrent Epidemics.. 3 David J.D. Earn 1.1
Mathematical Epidemiology 1 F. Brauer, P. van den Driessche and J. Wu, editors Part I Introduction and General Framework 1 A Light Introduction to Modelling Recurrent Epidemics.. 3 David J.D. Earn 1.1
The roadmap. Why do we need mathematical models in infectious diseases. Impact of vaccination: direct and indirect effects
 Mathematical Models in Infectious Diseases Epidemiology and Semi-Algebraic Methods Why do we need mathematical models in infectious diseases Why do we need mathematical models in infectious diseases Why
Mathematical Models in Infectious Diseases Epidemiology and Semi-Algebraic Methods Why do we need mathematical models in infectious diseases Why do we need mathematical models in infectious diseases Why
The Mathematics of Flu, Explained
 The Mathematics of Flu, Explained Richard C. Larson rclarson@mit.edu Massachusetts Institute of Technology Cambridge, Massachusetts 02139 USA September 5, 2009 Thank you for doing this exercise in your
The Mathematics of Flu, Explained Richard C. Larson rclarson@mit.edu Massachusetts Institute of Technology Cambridge, Massachusetts 02139 USA September 5, 2009 Thank you for doing this exercise in your
Modelling BCG vaccination in the UK: What is the impact of changing vaccination policy?
 Modelling BCG vaccination in the UK: What is the impact of changing vaccination policy? Sam Abbott Supervisors: Hannah Christensen, Ellen Brooks-Pollock University of Bristol 1 1. Lambert, M. L., Hasker,
Modelling BCG vaccination in the UK: What is the impact of changing vaccination policy? Sam Abbott Supervisors: Hannah Christensen, Ellen Brooks-Pollock University of Bristol 1 1. Lambert, M. L., Hasker,
Population Dynamics in the Presence of Infectious Diseases
 Population Dynamics in the Presence of Infectious Diseases Nurunisa Neyzi FINAL PROJECT QBIO, Spring 2009 INTRODUCTION INFECTIOUS DISEASES: Epidemic Endemic FACTORS: Sanitation and good water supply Human
Population Dynamics in the Presence of Infectious Diseases Nurunisa Neyzi FINAL PROJECT QBIO, Spring 2009 INTRODUCTION INFECTIOUS DISEASES: Epidemic Endemic FACTORS: Sanitation and good water supply Human
Mathematics of Infectious Diseases
 Mathematics of Infectious Diseases Zhisheng Shuai Department of Mathematics University of Central Florida Orlando, Florida, USA shuai@ucf.edu Zhisheng Shuai (U Central Florida) Mathematics of Infectious
Mathematics of Infectious Diseases Zhisheng Shuai Department of Mathematics University of Central Florida Orlando, Florida, USA shuai@ucf.edu Zhisheng Shuai (U Central Florida) Mathematics of Infectious
Infectious Disease Epidemiology and Transmission Dynamics. M.bayaty
 Infectious Disease Epidemiology and Transmission Dynamics M.bayaty Objectives 1) To understand the major differences between infectious and noninfectious disease epidemiology 2) To learn about the nature
Infectious Disease Epidemiology and Transmission Dynamics M.bayaty Objectives 1) To understand the major differences between infectious and noninfectious disease epidemiology 2) To learn about the nature
Behavior-Disease Models with respect to HIV Dynamics
 Behavior-Disease Models with respect to HIV Dynamics Aidan Grennell Western Carolina University 1 Abstract Expanding on the Susceptible-Infected-Recovered (SIR) epidemiological models, we review Towards
Behavior-Disease Models with respect to HIV Dynamics Aidan Grennell Western Carolina University 1 Abstract Expanding on the Susceptible-Infected-Recovered (SIR) epidemiological models, we review Towards
L4, Modeling using networks and other heterogeneities
 L4, Modeling using networks and other heterogeneities July, 2017 Different heterogeneities In reality individuals behave differently both in terms of susceptibility and infectivity given that a contact
L4, Modeling using networks and other heterogeneities July, 2017 Different heterogeneities In reality individuals behave differently both in terms of susceptibility and infectivity given that a contact
Modelling HIV prevention: strengths and limitations of different modelling approaches
 Modelling HIV prevention: strengths and limitations of different modelling approaches Leigh Johnson Centre for Infectious Disease Epidemiology and Research Background Models of HIV differ greatly in their
Modelling HIV prevention: strengths and limitations of different modelling approaches Leigh Johnson Centre for Infectious Disease Epidemiology and Research Background Models of HIV differ greatly in their
Chapter 15: Continuation of probability rules
 Chapter 15: Continuation of probability rules Example: HIV-infected women attending either an infectious disease clinic in Bangkok were screened for high-risk HPV and received a Pap test; those with abnormal
Chapter 15: Continuation of probability rules Example: HIV-infected women attending either an infectious disease clinic in Bangkok were screened for high-risk HPV and received a Pap test; those with abnormal
Mathematical modelling of infectious disease transmission
 Mathematical modelling of infectious disease transmission Dennis Chao Vaccine and Infectious Disease Division Fred Hutchinson Cancer Research Center 11 May 2015 1 / 41 Role of models in epidemiology Mathematical
Mathematical modelling of infectious disease transmission Dennis Chao Vaccine and Infectious Disease Division Fred Hutchinson Cancer Research Center 11 May 2015 1 / 41 Role of models in epidemiology Mathematical
0.1 Immunology - HIV/AIDS. 0.2 History & biology of HIV
 0.1 mmunology - HV/ADS n our previous models we assumed a homogeneous population where everyone was susceptible and infectious to the same degree. n contrast, the dynamics of STDs is affected by the general
0.1 mmunology - HV/ADS n our previous models we assumed a homogeneous population where everyone was susceptible and infectious to the same degree. n contrast, the dynamics of STDs is affected by the general
A Mathematical Model for the Transmission Dynamics of Cholera with Control Strategy
 International Journal of Science and Technology Volume 2 No. 11, November, 2013 A Mathematical Model for the Transmission Dynamics of Cholera with Control Strategy Ochoche, Jeffrey M. Department of Mathematics/Statistics/Computer
International Journal of Science and Technology Volume 2 No. 11, November, 2013 A Mathematical Model for the Transmission Dynamics of Cholera with Control Strategy Ochoche, Jeffrey M. Department of Mathematics/Statistics/Computer
Quantification of Basic Epidemiological Characteristics: The Example of Human Polyomaviruses. Georg A Funk University of Basel, Switzerland
 Quantification of Basic Epidemiological Characteristics: The Example of Human Polyomaviruses Georg A Funk University of Basel, Switzerland Outline Summary Discussion Results Learning goals Epidemiological
Quantification of Basic Epidemiological Characteristics: The Example of Human Polyomaviruses Georg A Funk University of Basel, Switzerland Outline Summary Discussion Results Learning goals Epidemiological
Infectious disease modeling
 Infectious disease modeling Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4500, Spring 2017 M. Macauley (Clemson) Infectious disease
Infectious disease modeling Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4500, Spring 2017 M. Macauley (Clemson) Infectious disease
Computer Science 101 Project 2: Predator Prey Model
 Computer Science 101 Project 2: Predator Prey Model Real-life situations usually are complicated and difficult to model exactly because of the large number of variables present in real systems. Computer
Computer Science 101 Project 2: Predator Prey Model Real-life situations usually are complicated and difficult to model exactly because of the large number of variables present in real systems. Computer
Structured models for dengue epidemiology
 Structured models for dengue epidemiology submitted by Hannah Woodall for the degree of Doctor of Philosophy of the University of Bath Department of Mathematical Sciences September 24 COPYRIGHT Attention
Structured models for dengue epidemiology submitted by Hannah Woodall for the degree of Doctor of Philosophy of the University of Bath Department of Mathematical Sciences September 24 COPYRIGHT Attention
Modelling Macroparasitic Diseases
 Modelling Macroparasitic Diseases Ben Collyer January 23, 2018 Ben Collyer Modelling Macroparasitic Diseases January 23, 2018 1 / 25 Parasitic worms Parasitic worms, also known as helminths, are able to
Modelling Macroparasitic Diseases Ben Collyer January 23, 2018 Ben Collyer Modelling Macroparasitic Diseases January 23, 2018 1 / 25 Parasitic worms Parasitic worms, also known as helminths, are able to
MODELLING INFECTIOUS DISEASES. Lorenzo Argante GSK Vaccines, Siena
 MODELLING INFECTIOUS DISEASES Lorenzo Argante GSK Vaccines, Siena lorenzo.x.argante@gmail.com GSK IN A NUTSHELL GSK VACCINES - GLOBAL PRESENCE SIENA RESEARCH AND DEVELOPMENT (R&D) SITE EXPLORATORY DATA
MODELLING INFECTIOUS DISEASES Lorenzo Argante GSK Vaccines, Siena lorenzo.x.argante@gmail.com GSK IN A NUTSHELL GSK VACCINES - GLOBAL PRESENCE SIENA RESEARCH AND DEVELOPMENT (R&D) SITE EXPLORATORY DATA
Mathematics Model Development Deployment of Dengue Fever Diseases by Involve Human and Vectors Exposed Components
 Volume-8, Issue-4, August 2018 International Journal of Engineering and Management Research Page Number: 46-53 DOI: doi.org/10.31033/ijemr.8.4.5 Mathematics Model Development Deployment of Dengue Fever
Volume-8, Issue-4, August 2018 International Journal of Engineering and Management Research Page Number: 46-53 DOI: doi.org/10.31033/ijemr.8.4.5 Mathematics Model Development Deployment of Dengue Fever
Biological Event Modeling for Response Planning
 Biological Event Modeling for Response Planning Clement McGowan, Ph.D. Fred Cecere, M.D. Robert Darneille Nate Laverdure Mitretek Systems, Inc. 3150 Fairview Park South Falls Church, VA 22042 mcgowan@mitretek.org
Biological Event Modeling for Response Planning Clement McGowan, Ph.D. Fred Cecere, M.D. Robert Darneille Nate Laverdure Mitretek Systems, Inc. 3150 Fairview Park South Falls Church, VA 22042 mcgowan@mitretek.org
Understanding Vaccine Economics with Simulations Authors: David Bishai and Sasmira Matta
 Understanding Vaccine Economics with Simulations Authors: David Bishai and Sasmira Matta Learning Objectives: To understand the Philipson effect or how the acceptability of a vaccine is determined To understand
Understanding Vaccine Economics with Simulations Authors: David Bishai and Sasmira Matta Learning Objectives: To understand the Philipson effect or how the acceptability of a vaccine is determined To understand
Matt Smith. Avian Flu Model
 Robert Smith? Patrick O Brian Matt Smith Avian Flu Model MAT3395 April 27, 2009 Objectives -Estimate the size of an outbreak if a shift occurred in the disease -determine if quarantine would be as effective
Robert Smith? Patrick O Brian Matt Smith Avian Flu Model MAT3395 April 27, 2009 Objectives -Estimate the size of an outbreak if a shift occurred in the disease -determine if quarantine would be as effective
EXERCISE: HOW TO DO POWER CALCULATIONS IN OPTIMAL DESIGN SOFTWARE
 ...... EXERCISE: HOW TO DO POWER CALCULATIONS IN OPTIMAL DESIGN SOFTWARE TABLE OF CONTENTS 73TKey Vocabulary37T... 1 73TIntroduction37T... 73TUsing the Optimal Design Software37T... 73TEstimating Sample
...... EXERCISE: HOW TO DO POWER CALCULATIONS IN OPTIMAL DESIGN SOFTWARE TABLE OF CONTENTS 73TKey Vocabulary37T... 1 73TIntroduction37T... 73TUsing the Optimal Design Software37T... 73TEstimating Sample
Technical Note 1 The Epidemiology of Mosquito-borne Diseases Prepared by Dr L. Molineaux
 Technical Note 1 The Epidemiology of Mosquito-borne Diseases Prepared by Dr L. Molineaux 1 Introduction Epidemiology is the science that describes and explains the distribution of disease in human populations:
Technical Note 1 The Epidemiology of Mosquito-borne Diseases Prepared by Dr L. Molineaux 1 Introduction Epidemiology is the science that describes and explains the distribution of disease in human populations:
Agent-Based Models. Maksudul Alam, Wei Wang
 Agent-Based Models Maksudul Alam, Wei Wang Outline Literature Review about Agent-Based model Modeling disease outbreaks in realistic urban social Networks EpiSimdemics: an Efficient Algorithm for Simulating
Agent-Based Models Maksudul Alam, Wei Wang Outline Literature Review about Agent-Based model Modeling disease outbreaks in realistic urban social Networks EpiSimdemics: an Efficient Algorithm for Simulating
PARASITE TRANSMISSION MODES AND THE EVOLUTION OF VIRULENCE
 Evolution, 55(12), 21, pp. 2389 24 PARASITE TRANSMISSION MODES AND THE EVOLUTION OF VIRULENCE TROY DAY Department of Zoology, University of Toronto, 25 Harbord Street, Toronto, ON M5S 3G5, Canada E-mail:
Evolution, 55(12), 21, pp. 2389 24 PARASITE TRANSMISSION MODES AND THE EVOLUTION OF VIRULENCE TROY DAY Department of Zoology, University of Toronto, 25 Harbord Street, Toronto, ON M5S 3G5, Canada E-mail:
VIRUS POPULATION DYNAMICS
 MCB 137 VIRUS DYNAMICS WINTER 2008 VIRUS POPULATION DYNAMICS Introduction: The basic epidemic model The classical model for epidemics is described in [1] and [Chapter 10 of 2]. Consider a population of
MCB 137 VIRUS DYNAMICS WINTER 2008 VIRUS POPULATION DYNAMICS Introduction: The basic epidemic model The classical model for epidemics is described in [1] and [Chapter 10 of 2]. Consider a population of
AGENT-BASED AND POPULATION-BASED SIMULATION: A COMPARATIVE CASE STUDY FOR EPIDEMICS
 AGENT-BASED AND POPULATION-BASED SIMULATION: A COMPARATIVE CASE STUDY FOR EPIDEMICS S. Waqar Jaffry and Jan Treur Vrije Universiteit Amsterdam, Department of Artificial Intelligence De Boelelaan 8, 8 HV
AGENT-BASED AND POPULATION-BASED SIMULATION: A COMPARATIVE CASE STUDY FOR EPIDEMICS S. Waqar Jaffry and Jan Treur Vrije Universiteit Amsterdam, Department of Artificial Intelligence De Boelelaan 8, 8 HV
Making comparisons. Previous sessions looked at how to describe a single group of subjects However, we are often interested in comparing two groups
 Making comparisons Previous sessions looked at how to describe a single group of subjects However, we are often interested in comparing two groups Data can be interpreted using the following fundamental
Making comparisons Previous sessions looked at how to describe a single group of subjects However, we are often interested in comparing two groups Data can be interpreted using the following fundamental
Next, your teacher will ask everyone who is infected to raise their hand. How many people were infected?
 Some Similarities between the Spread of an Infectious Disease and Population Growth by Jennifer Doherty and Dr. Ingrid Waldron, Department of Biology, University of Pennsylvania, 2007 1 How Does an Infectious
Some Similarities between the Spread of an Infectious Disease and Population Growth by Jennifer Doherty and Dr. Ingrid Waldron, Department of Biology, University of Pennsylvania, 2007 1 How Does an Infectious
Modeling of epidemic spreading with white Gaussian noise
 Article Statistical Physics and Mathematics for Complex Systems December 20 Vol.56 No.34: 3683 3688 doi: 0.007/s434-0-4753-z SPECIAL TOPICS: Modeling of epidemic spreading with white Gaussian noise GU
Article Statistical Physics and Mathematics for Complex Systems December 20 Vol.56 No.34: 3683 3688 doi: 0.007/s434-0-4753-z SPECIAL TOPICS: Modeling of epidemic spreading with white Gaussian noise GU
Thursday. Compartmental Disease Models
 Thursday Compartmental Disease Models Model Formulation Major decisions in designing a model Even after compartmental framework is chosen, still need to decide: Deterministic vs stochastic Discrete vs
Thursday Compartmental Disease Models Model Formulation Major decisions in designing a model Even after compartmental framework is chosen, still need to decide: Deterministic vs stochastic Discrete vs
Sawtooth Software. MaxDiff Analysis: Simple Counting, Individual-Level Logit, and HB RESEARCH PAPER SERIES. Bryan Orme, Sawtooth Software, Inc.
 Sawtooth Software RESEARCH PAPER SERIES MaxDiff Analysis: Simple Counting, Individual-Level Logit, and HB Bryan Orme, Sawtooth Software, Inc. Copyright 009, Sawtooth Software, Inc. 530 W. Fir St. Sequim,
Sawtooth Software RESEARCH PAPER SERIES MaxDiff Analysis: Simple Counting, Individual-Level Logit, and HB Bryan Orme, Sawtooth Software, Inc. Copyright 009, Sawtooth Software, Inc. 530 W. Fir St. Sequim,
Next, your teacher will ask everyone who is infected to raise their hand. How many people were infected?
 Some Similarities between the Spread of an Infectious Disease and Population Growth by Jennifer Doherty and Dr. Ingrid Waldron, Department of Biology, University of Pennsylvania, 2007 1 How Does an Infectious
Some Similarities between the Spread of an Infectious Disease and Population Growth by Jennifer Doherty and Dr. Ingrid Waldron, Department of Biology, University of Pennsylvania, 2007 1 How Does an Infectious
Project for Math. 224 DETECTION OF DIABETES
 Project for Math. 224 DETECTION OF DIABETES Diabetes is a disease of metabolism which is characterized by too much sugar in the blood and urine. Because of the lack of insulin (a hormone), the patient
Project for Math. 224 DETECTION OF DIABETES Diabetes is a disease of metabolism which is characterized by too much sugar in the blood and urine. Because of the lack of insulin (a hormone), the patient
Mathematical Modelling of Infectious Diseases. Raina MacIntyre
 Mathematical Modelling of Infectious Diseases Raina MacIntyre A little bit of EBM is a dangerous thing Research question: Does smoking cause lung cancer? Answer: I couldn t find a meta-analysis or even
Mathematical Modelling of Infectious Diseases Raina MacIntyre A little bit of EBM is a dangerous thing Research question: Does smoking cause lung cancer? Answer: I couldn t find a meta-analysis or even
MIGRATION, MINES AND MORES: THE HIV EPIDEMIC IN SOUTHERN AFRICA
 MIGRATION, MINES AND MORES: THE HIV EPIDEMIC IN SOUTHERN AFRICA John Hargrove Introduction to the Applications of Mathematics in Biology and Medicine AIMS, Muizenberg 2 July 2012 The colonial map of Africa
MIGRATION, MINES AND MORES: THE HIV EPIDEMIC IN SOUTHERN AFRICA John Hargrove Introduction to the Applications of Mathematics in Biology and Medicine AIMS, Muizenberg 2 July 2012 The colonial map of Africa
A Practical Approach to the Prevention and Control of Johnes Disease. R. J. Sibley BVSc HonFRCVS Myhealthyherd.com United Kingdom
 A Practical Approach to the Prevention and Control of Johnes Disease R. J. Sibley BVSc HonFRCVS Myhealthyherd.com United Kingdom dicksibley@aol.com Key messages Key elements of Johnes Management Principles
A Practical Approach to the Prevention and Control of Johnes Disease R. J. Sibley BVSc HonFRCVS Myhealthyherd.com United Kingdom dicksibley@aol.com Key messages Key elements of Johnes Management Principles
A SIR Mathematical Model of Dengue Transmission and its Simulation
 TELKOMNIKA Indonesian Journal of Electrical Engineering Vol. 12, No. 11, November 2014, pp. 7920 ~ 7926 DOI: 10.11591/telkomnika.v12i11.6488 7920 A SIR Mathematical Model of Dengue Transmission and its
TELKOMNIKA Indonesian Journal of Electrical Engineering Vol. 12, No. 11, November 2014, pp. 7920 ~ 7926 DOI: 10.11591/telkomnika.v12i11.6488 7920 A SIR Mathematical Model of Dengue Transmission and its
Probability II. Patrick Breheny. February 15. Advanced rules Summary
 Probability II Patrick Breheny February 15 Patrick Breheny University of Iowa Introduction to Biostatistics (BIOS 4120) 1 / 26 A rule related to the addition rule is called the law of total probability,
Probability II Patrick Breheny February 15 Patrick Breheny University of Iowa Introduction to Biostatistics (BIOS 4120) 1 / 26 A rule related to the addition rule is called the law of total probability,
Comparing Proportions between Two Independent Populations. John McGready Johns Hopkins University
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
Using SAS to Model the Spread of Infectious Disease Karl Mink, Mike Zdeb, School of Public Health, Rensselaer, NY
 Paper 174-29 Using SAS to Model the Spread of Infectious Disease Karl Mink, Mike Zdeb, University@Albany School of Public Health, Rensselaer, NY ABSTRACT An epidemic is the rapid and extensive spread of
Paper 174-29 Using SAS to Model the Spread of Infectious Disease Karl Mink, Mike Zdeb, University@Albany School of Public Health, Rensselaer, NY ABSTRACT An epidemic is the rapid and extensive spread of
Outcome Benefit of Design Weakness of Design
 Disease Detectives Exam Part 1 1. For each study design in the table below, put the letter corresponding to the outcome that can be calculated with that study design, benefit of that study design, and
Disease Detectives Exam Part 1 1. For each study design in the table below, put the letter corresponding to the outcome that can be calculated with that study design, benefit of that study design, and
Type and quantity of data needed for an early estimate of transmissibility when an infectious disease emerges
 Research articles Type and quantity of data needed for an early estimate of transmissibility when an infectious disease emerges N G Becker (Niels.Becker@anu.edu.au) 1, D Wang 1, M Clements 1 1. National
Research articles Type and quantity of data needed for an early estimate of transmissibility when an infectious disease emerges N G Becker (Niels.Becker@anu.edu.au) 1, D Wang 1, M Clements 1 1. National
A Brief History. A Brief History (cont.) February 1, Infectious Disease epidemiology BMTRY 713 (Lecture 7) mathematical Modeling for ID
 Infectious Disease Epidemiology BMTRY 713 (A. Selassie, DrPH) Lecture 7 Mathematical Modeling: The Dynamics of Infection Learning Objectives 1. Define what models mean 2. Identify key concepts in ID mathematical
Infectious Disease Epidemiology BMTRY 713 (A. Selassie, DrPH) Lecture 7 Mathematical Modeling: The Dynamics of Infection Learning Objectives 1. Define what models mean 2. Identify key concepts in ID mathematical
Identification of Tissue Independent Cancer Driver Genes
 Identification of Tissue Independent Cancer Driver Genes Alexandros Manolakos, Idoia Ochoa, Kartik Venkat Supervisor: Olivier Gevaert Abstract Identification of genomic patterns in tumors is an important
Identification of Tissue Independent Cancer Driver Genes Alexandros Manolakos, Idoia Ochoa, Kartik Venkat Supervisor: Olivier Gevaert Abstract Identification of genomic patterns in tumors is an important
Student Exploration: Disease Spread
 Name: Date: Student Exploration: Disease Spread Vocabulary: disease, epidemic, infect, infectious disease, pathogen Prior Knowledge Questions (Do these BEFORE using the Gizmo.) 1. Why do you think it is
Name: Date: Student Exploration: Disease Spread Vocabulary: disease, epidemic, infect, infectious disease, pathogen Prior Knowledge Questions (Do these BEFORE using the Gizmo.) 1. Why do you think it is
Bioterrorism and the Pandemic Potential
 Page 1 of 5 Bioterrorism and the Pandemic Potential March 7, 2013 1001 GMT Print 38 35 125 29 Text Size Stratfor By Rebecca Keller Periodic media reports of bird flu, a new SARS-like virus and a case of
Page 1 of 5 Bioterrorism and the Pandemic Potential March 7, 2013 1001 GMT Print 38 35 125 29 Text Size Stratfor By Rebecca Keller Periodic media reports of bird flu, a new SARS-like virus and a case of
Evaluating the Economic Consequences of Avian Influenza (1) Andrew Burns, Dominique van der Mensbrugghe, Hans Timmer (2)
 Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized 47417 Evaluating the Economic Consequences of Avian Influenza (1) Andrew Burns, Dominique
Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized Public Disclosure Authorized 47417 Evaluating the Economic Consequences of Avian Influenza (1) Andrew Burns, Dominique
measles? Abstract Introduction JUNE 2017 routine vaccination to 1 year old babies, and the second dose to
 December JUNE 2017 2018 causes brains How canwhat we keep thelizards world free of to change size? measles? Authors: Authors: Susan Crow, Meghan Pawlowski, Manyowa Meki, Joaquin Prada, Jess Metcalf, Lara
December JUNE 2017 2018 causes brains How canwhat we keep thelizards world free of to change size? measles? Authors: Authors: Susan Crow, Meghan Pawlowski, Manyowa Meki, Joaquin Prada, Jess Metcalf, Lara
Chapter 6 subtitles postsynaptic integration
 CELLULAR NEUROPHYSIOLOGY CONSTANCE HAMMOND Chapter 6 subtitles postsynaptic integration INTRODUCTION (1:56) This sixth and final chapter deals with the summation of presynaptic currents. Glutamate and
CELLULAR NEUROPHYSIOLOGY CONSTANCE HAMMOND Chapter 6 subtitles postsynaptic integration INTRODUCTION (1:56) This sixth and final chapter deals with the summation of presynaptic currents. Glutamate and
The Islamic University of Gaza- Civil and Environmental Engineering Department Public Health (EENV-5325)
 The Islamic University of Gaza- Civil and Environmental Engineering Department Public Health (EENV-5325) Lecture 3: Components of the infectious disease process By Husam Al-Najar Components of the infectious
The Islamic University of Gaza- Civil and Environmental Engineering Department Public Health (EENV-5325) Lecture 3: Components of the infectious disease process By Husam Al-Najar Components of the infectious
Modelling the Dynamic of the Foot-and Mouth Disease in England 2001
 Modelling the Dynamic of the Foot-and Mouth Disease in England 2001 Seminar on Veterinary Epidemiology Franz Rubel Budapest, 28 May 2003 Mathematical Epidemiology Group, Institute for Medical Physics and
Modelling the Dynamic of the Foot-and Mouth Disease in England 2001 Seminar on Veterinary Epidemiology Franz Rubel Budapest, 28 May 2003 Mathematical Epidemiology Group, Institute for Medical Physics and
Mathematical Modelling of Pulmonary and Extra-pulmonary Tuberculosis
 Mathematical Modelling of Pulmonary and xtra-pulmonary Tuberculosis ita H. Shah # and Jyoti Gupta * # Professor, Department of Mathematics, Gujarat University, Ahmedabad, Gujarat, India, Research Scholar,
Mathematical Modelling of Pulmonary and xtra-pulmonary Tuberculosis ita H. Shah # and Jyoti Gupta * # Professor, Department of Mathematics, Gujarat University, Ahmedabad, Gujarat, India, Research Scholar,
Section 3.2 Least-Squares Regression
 Section 3.2 Least-Squares Regression Linear relationships between two quantitative variables are pretty common and easy to understand. Correlation measures the direction and strength of these relationships.
Section 3.2 Least-Squares Regression Linear relationships between two quantitative variables are pretty common and easy to understand. Correlation measures the direction and strength of these relationships.
