COCHLEAR MODEL FOR NORMAL AND DAMAGED EARS
|
|
|
- Sibyl Scott
- 5 years ago
- Views:
Transcription
1 TEL AVIV UNIVERSITY THE IBY AND ALADAR FLEISCHMAN FACULTY OF ENGINEERING The Zandman-Slaner Graduate School of Engineering COCHLEAR MODEL FOR NORMAL AND DAMAGED EARS By Azaria Cohen THESIS SUBMITTED FOR THE DEGREE OF DOCTOR OF PHILOSOPHY SUBMITTED TO THE SENATE OF TEL-AVIV UNIVERSITY January 2006
2 TEL AVIV UNIVERSITY THE IBY AND ALADAR FLEISCHMAN FACULTY OF ENGINEERING The Zandman-Slaner Graduate School of Engineering COCHLEAR MODEL FOR NORMAL AND DAMAGED EARS By Azaria Cohen THESIS SUBMITTED FOR THE DEGREE OF DOCTOR OF PHILOSOPHY SUBMITTED TO THE SENATE OF TEL-AVIV UNIVERSITY This Research Work was Carried Out at Tel-Aviv University in The Faculty Of Engineering Under The Supervision of Prof Miriam Furst Yust January 2006 ii
3 To all who have helped me get to this point, especially to my family iii
4 Table of Contents Table of Contents List of Tables List of Figures Abstract Acknowledgements iv vii viii x xii Introduction 1 1 Cochlear anatomy and physiology: data and models Introduction Structure and function of the ear Cochlear models Transmission line cochlear models Two dimensional cochlear models Three-dimensional cochlear models Enhanced one dimensional cochlear models Structure and function of the outer hair cell Outer hair cell models Types of hearing loss Physiology of the damaged cochlea Motivation of the present study The Model Description Introduction Cochlear Fluid Dynamics iv
5 2.3 The Outer Hair Cell Model OHC Mechano - Electrical model OHC Apical Membrane Electrical Principle Variations Regulated Current Source Voltage Dependent Length OHC Pressure Contribution Frequency Domain Solution Frequency Domain Formulation Wave Number Function Representation Finite Difference Solution The Liouville Green Approximation Liouville Green Vs. Finite Difference Time Domain Solution Mathematical Preface Time Domain Computational Algorithm Spatial Domain Solution Time Step Modified Euler Method Error Control and Variable Step Size Method Convergence and Stability Time Solution Algorithm Summary Time Domain Simulation Computation Analysis Computation Accuracy Time Step Spatial Step Time Versus Frequency Simulation Simulation Results Introduction The Model Responses to a Sine Wave Comparison between models result and measured data Tuning Curves Comparison between models tuning curves and measurements Audiogram Simulations Variable γ Representation of the Dynamic Properties of Acoustic Signals v
6 6.9 Signal in Noise Discussion 132 A List of Symbols and parameters 136 Bibliography 138 vi
7 List of Tables 6.1 List of model Parameters Equal peak parameters A.1 List of symbols vii
8 List of Figures 1.1 Human ear, showing the outer,middle and inner ear Lateral view of a chinchilla cochlea Stylized mammalian cochlea Radial segment of the cochlea duct A generic depiction of the one dimensional formulation Simplified physical model of the cochlea Transmission line analog Zwicker s hardware implemented model Nobili,Turicchia, De poli and Main s model Geisler outer hair cell feedback model Outer Hair Cell arcuate pectinate zone model Allen forward transduction outer hair cell model A simple piezoelectric-like model of an outer hair cell Schematic illustration of OHC by Dallos and Evans Hearing loss due to inner or outer hair loss Cochlear model geometry An equivalent electrical circuit of the outer-hair cell Simplified OHC s electrical circuit model Transducer conductance of the mammalian outer hair cell Alternative Electrical circuit representing an outer hair cell in vivo OHC isometric force generation model viii
9 2.7 OHC s isometric force versus basolateral membrane voltage Condition of validity for WKB WKB vs. finite differences WKB vs. finite differences Time and spatial steps Flow chart of the time domain simulation Result accuracy - time step size for the sin wave Spatial resolution vs MSE Time versus frequency simulations Partition velocity patterns as function of different γ comparison between Ruggero et al measurements and our model Isointensity curves from Ruggero et al comparison between damping factor and γ factor Tuning curves Tuning curves comparison to measurement Basilar membrane and auditory-nerve tuning curves threshold estimation curves Plots of hearing loss with respect to audiograms Estimated hearing loss for decreasing γ over x Partition velocity responses patterns for random vector gamma Plots of hearing loss with respect for different standard deviation coefficient Response to chirp by normal and impair ear Spectrogram of the word Shen in Hebrew Response to the word shen Word shen in a noisy ambiance ix
10 Abstract Since the mid-1980s there have been rapid advances in our understanding of how the ear functions. The present shop talk now centers on cochlear amplifiers and motile sensory cells. The outer hair cells are the main component in these cochlear amplifiers. Cochlear hearing loss usually involves damage to the inner and outer hair cells. The outer hair cells are generally more vulnerable to damage than the inner hair cells. When outer hair cells are damaged, the active mechanism tends to be reduced in effectiveness or lost altogether. As a result, sensitivity to weak sounds is reduced and the basilar membrane responses are much more broadly tuned. An objective of this work was to explain hearing impairment by use of a cochlear model. This model incorporates an outer hair cell model in a one-dimensional cochlear model. The two models control each other through cochlear partition movement and pressure. Motivated by the evidence that the frequency range of the outer hair cell motile is wide while the outer hair cell basolateral membrane cutoff frequency is less than 1 khz, we assumed that the outer hair cell works as an all pass filter. In particular, we assumed that the current through the apical membrane is controlled by basilar membrane displacement and velocity. Two hypotheses to the mechanism underlying this current regulation were suggested. We made an additional assumption that the outer hair cell motility is transformed in to a fed back force, that operates on the cochlear partition, by a spring-like model. A computational model was driven both in the time and frequency domains. We used the time domain computational model to predict cochlear partition velocity x
11 xi responses to various signals, such as speech and chirp. The frequency domain computational model responses were more accurate but were restricted to steady state tone responses. An outer hair cell gain factor was defined to indicate the outer-hair cell contribution at each location along the cochlear partition. The model simulations revealed typical normal and abnormal excitation patterns according to the value of the gain factor. The model outputs were used to estimate normal and hearing-impairment audiograms. High frequency loss was predicted by the model when the gain of the outer hair cell was relatively small at the basal part of the cochlear partition. Phonal trauma audiograms were predicted by the model, when the gain of the outer hair cell is random along the cochlear partition. A maximum threshold shift of about 60 db was obtained at 4 khz. The model predicted typical phenomena of hearing loss. The time domain simulation can be used to predict other hearing phenomena such as masking, combination tones, and acoustic emissions, which remain for further research.
12 Acknowledgements I would like to thank Professor Miriam Furst for her many suggestions and constant support during this research. I am grateful to my parents and my wife for their patience and love. Without them this work would never have come into existence. Finally, I wish to thank the following fellows in our university laboratory: Vered Weise, for her wonderful work; Amnon Duvdevani, for his friendship and help in this research; Oren Bahat, for the outstanding work; and, also, my brother Yohai. Azaria Cohen January 30, 2006 xii
13 Introduction The issue addressed in this research is: Is an outer hair cell, mechano electrical model embedded in one dimensional cochlear model suitable for explaining normal and damaged ears? Loss of hearing represents a serious health issue. As aging occurs, hearing generally become progressively worse. By middle age all of us can expect to have a noticeable loss of hearing, with the top octave of the hearing range of our youth beginning to be eroded. Deafness results not only in a progressive reduction in sensitivity to sound, it causes serious problems in communication as well. Hearing loss results loss of ability to discriminate the pitch of a sound, and to distinguish intelligible speech in noisy environments. For young children who lose hearing either through illness or as a result of one of the many congenital forms of hearing loss, the effect on learning and development can be catastrophic unless early signs of deafness are detected and remedial measures taken. To make rational decisions about how best to detect, and even possibly to prevent deafness, it is necessary to understand how the hearing system functions. To understand how the ear can go wrong we must start by understanding the physiology of hearing, and how it operates when it is functioning normally. A model of the inner ear is important for understanding hearing and hearing loss. 1
14 2 Modelling is a potential shortcut to understand how the inner ear works. Computational modelling of the cochlea serves a number of specific purposes. The validation of existing hypotheses is of prime importance. In general, conceptual models are constructed as a means of translating reality into a structure that the mind perceives as an explanation. The computational model provides an accessory to the conceptual model that enables responses to be computed and compared to existing data. Hearing-impairment due to acoustic trauma or aging is mainly caused by outer hair cell loss [9]. In recent years significant progress has been made in understanding the contribution of the mammalian cochlear outer hair cells to the normal auditory signal processing. The outer hair cells (OHCs) act as amplifiers. They are metabolically activated, and their motion effectively changes the basilar membrane mechanical response [67]. In models that describe the outer hair cell activity, it is assumed that the OHC cilia displacement generates forces that act on the basilar membrane [26, 68, 28, 94, 3]. The contribution of the OHC to psychoacoustical performances was previously demonstrated by models that functionally included OHC activity. Those models predict normal behavior and degradation in the performances due to OHC loss [51, 49, 65]. A classical one-dimensional cochlear model has been modified to include the OHC activity. In a hardware model described by Zwicker [25], the OHC act as saturating nonlinear mechanical amplifiers which feed back to the vibration of the basilar membrane. OHC activity was included in cochlear models by nonlinear damping and/or nonlinear compliance and additional delays [16, 31]. Various properties that are associated with OHC s were predicted by these models; such as cochlear emissions [57, 16], and two tone suppression [12, 13, 87].
15 3 In this present research, an integrated basilar membrane - outer hair cell model is developed. An outer hair cell model is embedded in a one dimensional cochlear model. The two models control each other through cochlear partition movement and pressure. This model predicts various types of hearing impairments.
16 Chapter 1 Cochlear anatomy and physiology: data and models 1.1 Introduction This chapter commences with a brief review of cochlear anatomy and physiology and then progresses through the modeling of the cochlea. Most state of the art cochlear models include an embodiment of outer hair cells that have been shown to change length in response to transmembrane voltage. This electro motility is hypothesized to underlie a process of mechanical amplification that increases the ability of mammals to detect faint sounds by a hundredfold [9]. 1.2 Structure and function of the ear The mammalian ear is traditionally considered as composed of three parts, the outer, middle and inner ear, c.f. Figure 1.1. The outer ear is composed of the pinna and the auditory canal, or meatus. The pinna and meatus together create a broad resonance which enhances sound levels at the eardrum, relative to those obtained at the same point in free space, over the frequency range from about 1.5 to 5 khz. The pinna, 4
17 5 Figure 1.1: Human ear, showing the outer, middle, and inner ear. [14] head, and upper torso significantly modify the incoming sound at medium and high frequencies. Sound travels down the meatus and causes the eardrum, or tympanic membrane, to vibrate. The eardrum forms the boundary between the outer and middle ear. These vibrations are transmitted through the middle ear by three small bones, the ossicles, to a membrane covered opening in the bony wall of the spiral-shaped structure of the inner ear, the cochlea. This opening is called the oval window, and it forms the boundary between the middle and the inner ear. The major function of the middle ear is to ensure the efficient transfer of sound energy from the air to the fluids in the cochlea. In humans, transmission of sound energy through the middle ear is most efficient at frequencies between, 0.5 to 4 khz. The ossicles have minute muscles attached to them that contract when exposed to intense sounds. This contraction,
18 6 Figure 1.2: Lateral view of a chinchilla cochlea with a bony shell removed. Arrows indicate remnants of cochlear partition, helicotrema, modiolus, oval window, round window, stapes, scala vestibuli and scala tympani [84]. known as the acoustic reflex, is probably mediated by the neural centers in the brain stem. The inner ear (the cochlea) consists of a fluid filed duct that is coiled like a snail shell and is embedded in bone c.f. Figure 1.2. The spiral shape does not appear to have any functional significance, and the cochlea is often described as if the spiral had been uncoiled. The cochlea is portrayed as having a longitudinal dimension, a vertical dimension, and a radial dimension that corresponds to the width of the duct when the cochlea is uncoiled. The cochlea is divided into three compartments, or scalae, by two longitudinal membranes. The upper membrane - Reissner s membrane - divides the scala vestibuli above from the scala media below; while the lower membrane - the basilar membrane - separates the scala media from the scala tympani c.f. Figure 1.3. Inward movement
19 7 Figure 1.3: Stylized mammalian cochlea, shown as if the cochlear partition were straight [14]. of the oval window results in a corresponding outward movement in a membrane covering a second opening in the cochlea, the round window. Such movements result in pressure differences between both sides of the basilar membrane. This results in movement of the basilar membrane c.f. Figure 1.4. The helicotrema, a small hole at the apical end that joins together the scala vestibuli and tympani, eliminates any pressure differences between the scalae at very low frequencies. The basilar membrane is attached to a bony shelf - the spiral lamina - on its inner edge, and to the specialized tissue called spiral ligament on its outer edge. The width of the cochlear duct and the spiral lamina decreases from base to apex, while the width of the basilar membrane increases from base to apex. A third membrane - the tectorial membrane - lies above the basilar membrane and also runs along the length of the cochlea. Between the basilar membrane and the tectorial membrane are hair cells, which form a part of a structure called the organ of Corti. They are called hair cells because they appear to have tufts of hairs, called stereocilia, at their apexes. The hair cells are divided into two groups by an arch
20 8 Figure 1.4: Radial segment of the cochlea duct, showing all three scalae. known as the tunnel of Corti. The outer hair cells are arranged in up to five rows in humans, and three rows in cats. The inner hair cells form a single row. In the human ear, there are about outer hair cells, each with 140 stereocilia protruding from it, whereas there are about 3500 inner hair cells, each with about 40 stereocilia. The outer hair cell stereocilia appears to make contact with the tectorial membrane, but this may not be valid for the inner hair cells. The tectorial membrane appears to be hinged at one side. When the basilar membrane moves up and down, a shearing motion is created, and the tectorial membrane moves to the side relative to the tops of the hair cells. As a result, the stereocilia at the top of the hair cells move sideways. The movement of the stereocilia leads to flow of electrical current through
21 9 the hair cell which, in turn, leads to the generation of action potentials. These potentials give rise to nerve spikes in the neurons of the auditory nerve. The inner hair cells act to transduce mechanical movement into neural activity. In the outer hair cells these potentials result in a change in both the length and stiffness. The outer hair cell activity is partly under the control of higher centers of the auditory system. The efferent nerve fibres innervate the outer hair cells and control their functionality. [26, 14]. 1.3 Cochlear models The first recognized model of the cochlea was published by Helmholtz in 1862 [36] in an appendix of On Sensation Of Tone. Helmholtz linked the cochlea to a bank of highly tuned resonators, which were selective for different frequencies, much like a piano or a harp, with each resonator representing a different place on the basilar membrane. The model he proposed is not very satisfying, however, since many important features were omitted. The most important of which includes the cochlear fluid which couples the mechanical resonators together. But, given the publication date, it is an impressive contribution by this early great master of physics and psychophysics. The next major contribution was made by Wegel and Lane [81], and is in a class of its own even today. The paper was the first to quantitatively describe the details of the upward spread of masking, and propose a modern model of the cochlea. If Wegel and Lane had been able to solve their model s equations, they would have predicted cochlear traveling waves [43]. It was the experimental observations of G. Von Békésy, starting in 1928 on the
22 10 cochleae of human cadavers, which unveiled the physical nature of the basilar membrane traveling wave [30]. Von Békésy, found that the cochlea is analogous to a dispersive transmission line where the different frequency components of which the input signal is comprised travel at different speeds along the basilar membrane; thereby isolating those various frequency components at different locations along the basilar membrane. He properly named this dispersive wave a traveling wave. He observed the traveling wave using stroboscopic light in dead human cochleae at sound levels well above the pain threshold, namely above 140 db SPL. These high sound pressure levels were necessary to obtain displacement levels that were observable under his microscope. Von Békésy s pioneering experiments were considered so important that in 1961 he was awarded the Nobel prize. Over the intervening years these experiments have been greatly improved, but Von Békésy s fundamental observations of the traveling wave still stand. Today, it is found that the traveling wave has a more sharply defined location on the basilar membrane for pure tone input than observed by Von Békésy. In fact, according to measurements made over the last 20 years, the response of the basilar membrane to a pure tone can change in amplitude by more than five orders of magnitude per millimeter of distance along the basilar membrane [43]. To describe this response it is helpful to call upon the transmission line model, which was first quantitatively analyzed by Zwislocky [48], Peterson and Bogart [55] and Fletcher [35]. The transmission line model is also called the one dimensional model, or long wave model.
23 11 Figure 1.5: A generic depiction of the one dimensional formulation [26] Transmission line cochlear models Zwislocki [47] was the first to quantitatively analyze Wegel and Lane s [81] cochlear model, explaining Von Békésy s traveling wave. Wegal and Lane s cochlear model is constructed from cascade sections of inductors, capacitors, and resistors; which represent the mass of the fluids of the cochlea and the basilar membrane mass, partition resistance and stiffness, respectively. Figure 1.5 shows an acoustic impedance analog superimposed over the cochlear scalae. A segment of length x is depicted as a single collection of elements at location x. The incremental aspects of the vertical and width dimensions have been suppressed; which is equivalent to saying that a particular variable as a function of x is constant from top to bottom and from side to side. The acoustic impedance of a segment, x, of fluid in the channels is represented
24 12 Figure 1.6: one dimension model: from Zweig et al [32], simplified physical model of the cochlea as an inertial term L s = ρ x/a where A is the area of the scala and ρ is the fluid density. A spring C CP (x), a mass L CP (x), and a damper R CP (x) (small frame in Figure 1.5), referenced over the surface area of the incremental portion, represent the acoustic impedance of the cochlear partition x. In most transmission line models, the fluid is considered as incompressible. In a one-dimension model, parameters can be easily chosen using methods that make sense anatomically, physiologically, and mechanically [26]. In 1976, George Zweig and colleagues [32], noted that an approximate, but accurate, solution for the one dimensional model shown in Figure 1.6 and Figure 1.7 could be obtained using a well known method in physics called the Liouville Green or WKB approximation [32]. Subsequently, the method was widely adopted [60]. The results of Zweig et al [32] were similar to Rhode s contemporary neural tuning curve responses [92].
25 13 Figure 1.7: one dimension model: from Zweig et al [32], transmission line analog for a section of the cochlea of length x Two dimensional cochlear models The need for a two-dimensional theory was first explicitly presented by Ranke [66]. In the 70 s, several two- dimensional model solutions became available. Ranke was the first to formulate and consider a two-dimensional model. He emphasized that near the point of maximum amplitude of the basilar membrane, the fluid velocity component perpendicular to the membrane should not be neglected with respect to the longitudinal component. He argued that the long wave approximation is valid only so long as λ 2πh, where λ is the length of the wave propagation along the membrane, and h is the scala height. He showed that the parameter values of the pertinent quantities are such that this condition is certainly not fulfilled in the region of maximum response of the membrane. As opposed to the long wave approach, Ranke regarded the channel height as
26 14 infinitely large, thus arriving at a deep water, or short wave, approximation. This enabled him to construct a solution that resembles the actual solution of the twodimensional model in the region of maximum amplitude. Far basal to this region the deep water approximation is not accurate, so he advised using the long wave approach in that area. The apical part of the cochlea can be disregarded since the membrane displacement is practically zero there. The two-dimensional model is considered to be theoretically more natural than the long wave theories; however, the reason that long wave models have gained more appreciation than the short wave approach is perhaps because they are easy to understand and simple to solve numerically Three-dimensional cochlear models The dimension lateral to the cochlear partition seems the least important in determining the basilar membrane response to stapes movements. In the three-dimensional model, the pressure and fluid flows can vary across the width (the radial dimension) of the cochlea partition. This pressure variation is consistent with the notion that the basilar membrane have different mechanical properties along the cochlear partition. In light of the obvious possibilities afforded by the three-dimensional model formulation, early works on the three-dimensional model ignored three dimensional variation in the physical properties of the cochlear partition [60]. Much of the three-dimensional model work involved complicated mathematics [18, 83] and [19] required simplifying assumptions which ignored much of the physiological reality of the cochlea [26]. An exception was the work of Tabar and Steele [19], who augmented their three-dimensional model formulations to include abstractions of anatomically relevant structures. Lien and Cox [64] made simplifying assumptions and collapsed the three-dimensional
27 15 model formulation to a one-dimensional model formulation. The interpretation of the Lien and Cox model is that it is possible to use a one-dimensional model with some modifications in order to mimic the three-dimensional model. Potentially, this gave credibility to the one-dimensional model approach. The discoveries of the nonlinear compressive basilar membrane and inner hair cell responses [92], the oto acoustic emission [23], and the outer hair cell motility [90] brought about a paradigm shift. Today we know that the discoveries in the 70 s and 80 s are related, and involved outer hair cells. These discoveries cannot simply be explained with a linear model. A new branch of extended models was called for Enhanced one dimensional cochlear models The large number of nonlinear phenomena discoveries, which began in the 70 s, revealed the necessity of incorporating nonlinear elements in the cochlear models. The equations of the nonlinear model cannot be solved by Fourier transform, i.e. in the frequency domain. A way to solve these equations is by computer modeling; another way is by use of an electric analogue circuit. In computer modeling, the one-dimensional model simulations require less memory and fewer operations than the two-dimensional and three-dimensional models. This is reasonable since all the one- dimensional hydrodynamic formulations have fewer components to deal with. Several works have utilized two-dimensional computer modeling; an example can be found in Diependaal and Viergever [79]. However, the rest of this section considers only one-dimensional models. Hubbard s model [4] and Hall s model [50] both use nonlinear damping that increases as the level of the cochlear partition velocity increases. The major shortcoming was that the filter quality factor (Q factor) of the tuned sections had to be increased
28 16 so that the nonlinearity could have the desirable effect of subsequently reducing the filter quality factor in a way that agreed with the data. This caused the model output, the velocity or displacement along the cochlea partition, to have tips that were too sharp at low stimulus levels, although they were reasonable at higher sound levels [26]. Other studies indicated that nonlinear damping alone could not account for cochlea data [57]. Furst and Goldstein [57], tested a nonlinear damping model versus a nonlinear damping and stiffness model. The latter was necessary to explain both the amplitude and phase of the cubic distortion product 2f 1 f 2. A very interesting and inspired cochlea model was proposed by Hubbard and Mountain [5]. They suggested a nonlinear traveling-wave amplifier model of the cochlea, based on Hubbard s traveling-wave model [4]. Hubbard s model is comprised of two transmission lines, coupled tightly by feedback. The traveling wave obtained by a classical one dimensional model slows down in the characteristic frequency region to approximately match the natural propagation velocity of the second line. When this takes place, amplification occurs. A fundamental difference between this model and many other active models is that power is generated principally in the tip region of the response; not in the region basal to the tip. Hubbard s original model has been changed so that inter-line coupling function is nonlinear. A modification of this model that includes a representation of the electrical characteristics of the scala media and the outer hair cells (OHCs) was represented by Hubbard et al [6]. This model represents two modes of traveling wave propagation in the cochlea using two coupled transmission lines; one of which is a standard one-dimensional model of the transverse motion of the cochlear partition. The other line represents hydromechanical changes in the organ of Corti. The coupling from the first line (the cochlear partition model)
29 17 to the second line is through a circuit that represents the electrical properties of the scala media and the OHCs. A nonlinearity is added into the model by introducing a saturated conductance as part of the hair cell apical membrane functionality. This conductance varies as a function of the basilar membrane displacement. Perturbations in this conductance cause variations in the basal hair cell trans-membrane voltage. These variations are coupled to the first line by changes in OHC motility. A hardware model of the nonlinear preprocessing established in the inner ear was described by Zwicker [25]. The schematic diagram is shown in Figure 1.8. This model is based on the assumption that the outer hair cells act as saturating nonlinear mechanical amplifiers which feedback to the vibration of the basilar membrane; while only the inner hair cells transfer information toward higher centers. Zwicker s model contains activity, feedback, and nonlinearity. In Zwicker s model, the hydrodynamic one-dimensional model is implemented as a transmission line. Zwicker s OHC model is composed of an amplifier and sigmoidshaped nonlinear compressor which is stimulated with a RLC circuit with a transformer. The output of the compressor is fed back to the transmission line through the same transformer. The model was able to predict inner hair cell neural activity resulting from the input signal. Its major shortcoming is the relatively small number of sections, only 90. The differences between the adjoining sections impedances are relatively large, which results in too many reflections. The complexity of the mechanical structure of the scala media and the organ of Corti inspired some researchers to develop more advanced models. Nobili et al [54, 74] suggested a model of the outer hair cells and the tectorial membrane structure that
30 Figure 1.8: Zwicker s hardware model [25]. A block diagram of one section out of 90 sections. (a) is normally used electrical circuit of the hydromechanics of the inner ear. (b) is a dual circuit of (a) with driving and load impedances at the two ends of the line. The outer hair cell circuit is fed by the basilar membrane velocity and results in the amplification of the basilar membrane velocity 18
31 19 enhances partition motion and frequency selectivity. One section of Nobili et al. model is depicted in Figure 1.9. This model is made of an array of non-linear oscillators, each of which is coupled instantly to all the others through hydrodynamic forces transmitted by the fluid that fills its interior. The input to the cochlea through the ossicle chain of the middle ear is also transmitted hydrodynamically to the oscillator array. Owing to the different physical parameters of the oscillators (mass, stiffness and damping constants), the response of the array to a frequency tone, peaks at a frequency dependent location within the cochlea. A typical response is a traveling wave, characterized by a phase delay that increases monotonically along the oscillator array, accumulating a few cycles up to the location of the response peak. Physically, each oscillator is realized by a segment of the cochlear partition contained between the elastic basilar membrane and the tectorial membrane [54, 74]. The nonlinearity is expressed by a sigmoid function operating on the basilar membrane velocity, and feed back pressure difference on the basilar membrane. The model of Nobili et al., can be viewed as a nonlinear damping factor model. For low stimulus levels, the OHC force decreases the partition damping factor and therefore improves frequency selectivity and hearing system sensitivity. In another work by Nobili, Mammano and Ashmore [74], a shearing viscosity term was added. This term represents the viscous forces acting on one oscillator section, caused by possible different velocities of adjacent oscillators. The tectorial membrane to basilar membrane mutual displacement is controlled by the outer hair cells. The idea is generally accepted that there must be another component that enhances location specific frequencies, other than the transmission line filters that enhances location
32 20 Figure 1.9: Nobili,Turicchia, De poli and Main s model [54], mechanical equivalent of an oscillating unit of the cochlea partition specific frequencies. Hubbard [6], Zwicker [25], Nobili [74] and the work of others, utilize this idea from different points of view. In an effort to explain Rhode s [92] finding of the differences between basilar membrane tuning curves in the simple one-dimensional model and neuronal excitation patterns, some investigators hypothesize that the shear between the reticular lamina and the tectorial membrane is enhanced by a second filter. Allen [41] suggested a second filter model. According to this concept, the neural excitation is simply related to the reticular lamina tectorial membrane shear. Allen developed a transduction filter based on micromechanics and included this transduction function in a hydromechanical model [44]. To obtain the filter
33 21 characteristics, the basilar membrane and the tectorial membrane were represented as resonant structures coupled by viscoelastic stereocilia. The tectorial membrane essentially vibrated in a radial dimension while the basilar membrane vibrated up and down. Allen suggested models in which the outer hair cells do not provide power amplification to the basilar membrane traveling wave [43]. Allen s model is an example in which a passive model can explain the sharp neural excitation pattern. Active and passive models currently represent two alternative and competitive explanations for cochlear mechanics. Active models contain power sources while passive models do not. In practice, this distinction between active and passive is not quite clear. In some sense, passive models are active, for example, stiffness changes can cause motion resulting in a power source. From an energetic point of view, the OHC s operation consumes energy that, in part, is spent as mechanical power. The resonant tectorial membrane model is not active in the sense that outer hair cells provide power amplification to the basilar membrane traveling wave. The resonant tectorial membrane (RTM) model is made nonlinear by control of the basilar membrane stiffness via OHCs stiffness (or length changes) [42]. The basal end of each OHC is attached to the basilar membrane via an interlaced chain of Dieter cells. Attached to the apical end of the OHCs are the cilia, the longest row of which are connected to the tectorial membrane. It is postulated that the decrease in OHC stiffness that accompanies cilia stimulation results in a decrease of the net partition stiffness (increasing compliance). This decrease in the local basilar membrane stiffness results in the partition excitation pattern shifting basally towards the stapes.
34 22 Another way to view this is that at any point along the basilar membrane the resonant frequency decreases with increasing intensity. This migration of the excitation pattern, combined with the assumption that the tectorial membrane has a high pass characteristic, means that the cilia excitation gain at characteristic frequency is nonlinearly compressed as the intensity increases [43]. The passive models cannot produce cochlear partition movement from a rest condition. Although the models can be nonlinear, it is obvious that if there is no stimuli then the partition will remain at rest. Thus, these models cannot explain the well known phenomenon of spontaneous oto acoustic emission (SOAE) - the phenomenon wherein sound is emitted from the inner ear spontaneously. In most cases, SOAE presence is a sign of a healthy cochlea. The Talmadge, Long, and Tubis model [91] predicts SOAE. This model incorporates nonlinearity in terms of a Van Der Pol oscillator. The nonlinear term was added to the damping factor in the equation of motion Eq: The Van Der Pol oscillator is shown by: p + ( r 1 + r 2 p 2 )ṗ + ω 0 p = 0 (1.3.1) which is very similar to the equation of motion. The parameters r 1, r 2 are small positive numbers. A solution to this differential equation is given by: p cos(ω 0 t + ϕ 0 ) (1.3.2) which means that it produces oscillations although no stimulus exists. There are two processes involved in the damping factor of the Van Der Pol oscillator. The first process is a negative resistor, and is due to the outer hair cell counter damping force.
35 23 The second process is a nonlinear saturated term, that increases as a function of the basilar membrane motion.hence, if a section impedance is viewed as a Van Der Pol oscillator, its oscillations spread through the cochlear fluid; resulting in SOAE. The Van Der Pol nonlinear oscillator principle was modified by Talmadge, Tubis, and Long in a series of papers [15, 16, 17]. Their models use the concept of delayed operation, as suggested by Zweig [31]. Zweig has shown that the damping factor acts like a negatively damped harmonic oscillator stabilized by a feedback force proportional to the velocity at some previous time. He did this by extrapolating the basilar membrane velocity versus the umbo velocity, and then solving the inverse problem. This means that he found the model assumptions which can obtain that transfer function. Moreover, the concept of delayed feedback was expanded to two kinds of delayed force; fast feedback and slow feedback. Another model of the outer hair cell motility that cooperated with a cochlear model was suggested by Geisler [12, 13]. Figure 1.10 depicts a schematic representation of Geisler s model. Two free bodies equations, for the basilar membrane and reticular lamina, were described: body 2 body 1 {}}{{}}{ F a = k b x + mẍ + rẋ F m + k r (x y) (1.3.3) 0 = F m + k c y + k r (y x) The outer hair cell force frequency transform was described as an all-pass filter with a constant delay [31, 13]. Most of the models that demonstrate sharpening in the basilar membrane velocity curves due to decreases in the cochlear partition damping factor exhibit non realistic
36 24 Figure 1.10: Geisler s outer hair cell feedback model [11, 12], This picture was taken from [12]. Shown here is the basic outer hair cell feedback model of the cochlear partition radial cross section. In this drawing, tonal acoustic force F a displaces the basilar membrane upward by x units. The cilia tuft of the outer hair cell is deflected, causing a reaction force F m that acts upon both basilar membrane and reticular lamina. The total deflection of the reticular lamina is y units. responses. In order to obtain proper basilar membrane velocity curves, the energy injected by the outer hair cells has to be placed prior to the characteristic frequency site along the cochlear partition. But this configuration results in high level of energy injection by the outer hair cells. Kolston et al [71] were concerned by the large amounts of power used by active models. They suggested that the sharpening effect of cochlear amplifiers may be due to variable impedance. This impedance is connected in parallel to the partition mass, stiffness, and damping. In another earlier work, Kolston et al [72] suggested two mechanical modes of the cochlear partition. The partition is divided into arcuate zone and a pectinate zone. Figure 1.11 depicts the principle elements of this model. The Kolston et al formulation is that of the arcuate zone and the pectinate zone,
37 25 Figure 1.11: outer hair cell arcuate pectinate zone model [72]. Cross section schematic of the cochlea partition. The basilar membrane is divided into two zones, with the organ of Corti and the tectorial membrane influencing the mechanics of the arcuate zone. each responding to the pressure difference across the cochlear partition. Each zone is modeled as a spring mass damper combination. However, the arcuate zone impedance contains a hair cell component that gives the arcuate zone model response a realistic shape. The arcuate zone affects the partition impedance mostly in the region near the characteristic frequency. The outer hair cell stiffness is assumed to dominate the impedance of the arcuate region in cochlear regions basal to the characteristic place for a given frequency. To make the model applicable to all cochlear regions, and for all acoustic frequencies, the stiffness was allowed to be a function of both frequency and displacement, such that the resulting impedance was a frequency dependent reactance and a frequency dependent resistance. The effect of the pectinate zone was to reduce the responsiveness of the basilar membrane in the tail region (for lower frequencies) but not in the tip, such that the remaining peak was broad, and the tip to tail ratio
38 26 was in approximate agreement with data. There is a wide range of functional cochlear models. Lyon [78] described an auditory model based on a transmission line model of the basilar membrane, followed by several stages of adaptation. The cochlear model described by Lyon combines a series of filters that model the traveling pressure waves with Half Wave Rectifiers (HWR) to detect the energy in the signal and several stages of Automatic Gain Control (AGC). The outputs of the AGC stage are positive signals that indicate the firing rate of the neurons leading to the brain. The cochlea is divided into a large number of discrete sections. Each section is modeled as a simple linear transfer function. The model implementation uses approximately 80 stages. The cochlea model described by Lyon combines a series of notch filters that model the traveling pressure waves with resonators to model the conversion of pressure waves into basilar membrane motion or velocity. Patterson [77] proposed a model of psychoacoustic filtering based on critical bands. This auditory front-end utilized a Gammatone filter bank. The Gammatone auditory filter can be described by its impulse response: h(t) = at n 1 exp( 2πbt)cos(2πf c t + φ) for t 0. The primary parameters of the filter are b and n. b largely determines the duration of the impulse response; n is the order of the filter and it largely determines the slope of the skirts of the filter. When the order of the filter is in the range 3-5, the shape of the magnitude characteristic of the Gammatone filter is very similar to that of the roex(p) filter commonly used to represent the magnitude characteristic of the human auditory filter [77]. Glasberg and Moore [10] have summarized human data on the equivalent rectangular bandwidth (ERB) of the auditory filter with the function: ERB = f c. Together, the
39 27 last two equations define a Gammatone auditory filter bank if one includes the common assumption that the filter center frequencies are distributed across frequency in proportion to their bandwidth. When the order of the filter is 4, b = 1.018ERB. The 3-dB bandwidth of the Gammatone filter is times the ERB [77]. A Gammachirp auditory filter was developed by Irino and Patterson [88] to provide a leveldependent version of the linear, Gammatone auditory filter, with which to explain the level-dependent changes in cochlear filtering observed in psychophysical masking experiments. In this analytical Gammachirp filter, the chirp varied with level and there was no explicit representation of the change in filter gain or compression with level. Irino and Patterson suggested another form of the Gammachirp filter in which the magnitude response, the gain, and the compression vary with level while the chirp does not [89]. From the above review of cochlear models and from many other models, reviewed in [26], it is clear that the outer hair cells play an important role in cochlear mechanics. Their significance is whether the model assumes that they emit energy, or that they change the partition motion. The outer hair cells sense the partition vibration and enhance it by emitting energy directly, or by changing the partition mechanical properties. From the known data about outer hair cells, it is clear that the outer hair cell acts as a transducer. OHC transform cilia movement into electrical voltage, and electrical voltage into a mechanical change which results in an enhanced partition vibration.
40 Structure and function of the outer hair cell The outer hair cell shape is cylindrical, and its several rows of stereocilia have uniformly staggered height. The base of each outer hair cell is cradled by a single Deiter cell, leaving its lateral wall largely free of cellular contact, directly exposed to the perilymph that surrounds the organ of Corti. An outer hair cell is approximately 10µm in diameter, but its length changes as a function of its cochlear location. In cochlear regions tuned to low frequencies near the apical part of the partition, the outer hair cell length is greater than the length of the cell near the stapes. The outer hair cell length range is 10 90µm. Reissner s membrane separates the scala vestibuli from scala media and appears to serve as an ionic barrier between them. The fluid in the scala vestibuli and scala tympani, called perilymph, is characterized by ionic composition similar to the cerebrospinal fluid. It is high in Na + and low in K +. However, the ionic composition of the endolymph in the scala media is more similar in concentration to intracellular fluid. It is high in K + and low in Na +. The fluid in the scala media has electrical potential which is 90 mv more positive than that of scala vestibuli and scala tympani. The apical membranes of the hair cells and some of the supporting cells in the organ of Corti are tightly joined together to form a plate like structure on top of the organ of Corti, called the reticular lamina. These tight junctions form an ionic barrier between the scala media and the organ of Corti. In contrast, the basilar membrane appears to be reasonably permeable to ions, with the result that the ionic composition of the fluid within the organ of Corti is very similar to that of perilymph. There is a large voltage drop across the apical surface of the hair cell. From one side there is a large positive endo cochlear potential and on the other side there is
41 29 a negative intracellular potential 80mv. Therefore, the apical surfaces of both inner and outer hair cells have large voltage differences across them, greater than ( 100mv). These huge transmembrane potentials force mostly K + cations to flow into the apical section of each hair cell. Cochlear hair cells are epithelial cells, i.e. they are sealed between two different fluid compartments. They have two parts that behave differently. The apical part is surrounded by endolymph, and the basolateral part is surrounded by perilymph and supporting cells. The apical part of the cell contains the stereocilia, which give the hair cells their name. It is the deflection of these fine hairlike structures that delivers mechanical energy into the hair cell. What appears to be happening in hair cells is that there are shearing motions or displacement of these cilia. Adjacent stereocilia are connected to one another with extremely fine filaments, tip links, arranged along the major axis of the stereocilia bundle. The most commonly accepted hypothesis about these connections is that, when the stereocilia bundle is bent by mechanical force, these tip links are stretched as mechanical energy is delivered to them. When the mechanical energy is sufficiently large, the tip links physically open ion channels located somewhere in the stereocilia. This permits the abundantly available potassium ions from the endolymph to flow into the cell and change its electrical configuration, producing a voltage drop on the cell membrane. This is often referred as the receptor current. The receptor current flows down its gradient into the surrounding fluid. As it does, its produces a voltage drop on the cell basolateral membrane. This is called the receptor potential [67]. Displacement of the basilar membrane toward scala tympany results in rotations
42 30 of the stereocilia toward the limbus that produces hyperpolarization of the receptor potential. When the basilar membrane moves towards the scala vestibuli it produces depolarization of the hair cell. In 1983 Brownell et al [90] discovered that isolated outer hair cells change in length when their electrical environment changes. When an outer hair cell is isolated and depolarized, the cell becomes more positive inside, then it becomes shorter and thicker. When the cell is hyperpolarized it becomes longer and thinner [76]. This shape change is not trivial. It can be as large as 5% of the length of the cell [43]. The most popular theory is that the outer hair cell motility is due to molecules within its plasma membrane [26]. According to this theory, in a hyperpolarized cell these molecules are packed together in one particular configuration. With increasing levels of depolarization, increasing numbers of these particles undergo conformal changes that reduce their effective diameter or increase their packing density, thus the surface area of the cell accordingly shrinks. Thus, displacement of the basilar membrane toward scala vestibuli results in depolarization of the hair call; therefore, the hair cell undergoes contraction and hence, the basilar membrane is pulled toward the scala vestibuli. This process amplifies the partition movement toward the scala vestibuli. A similar process moves the cochlear partition toward the scala tympani. The outer hair cell undergoes elongation that pushes the basilar membrane toward the scala tympani. Outer hair cells undergo a somatic elongation-contraction cycle when electrically stimulated. This electro-motile response is assumed to underlie the high sensitivity and frequency selectivity of amplification in the mammalian cochlea. This process, presumably operating on a cycle by cycle basis at the frequency of the stimulus, is
43 31 believed to provide mechanical feedback to the basilar membrane motion. There is strong evidence that the outer hair cell motile frequencies are in the same range as basilar membrane displacement frequencies. In isolated voltage clamped cells the OHC easily follows sinusoidal electrical commands at frequencies up to 1kH. Externally applied electrical signals have been observed to drive the cells at frequencies up to 24kH [70]. However, if driven by the receptor potential of the cell, the mechanical feedback is expected to be severely attenuated at high frequencies because of electrical low-pass filtering by the outer hair cell basolateral membrane. 1.5 Outer hair cell models The outer hair cell transforms its cilia movement into structural changes such as elongation and elasticity. It is most probable that other changes, such as chemical and electrical changes, also occur in the OHC vicinity. The model assumes that the membrane electrical potential is developed due to OHC s cilia motion. Furthermore, a force is generated by the outer hair cell as a result of the electrical potential change. Davis [34], first proposed that hair cell mechano-electric transduction is the result of conductance change in the apical membrane caused by movement of the sensory hairs. It is presently known that hair cells in the cochlea have more than one type of mechanically sensitive conductance in their membranes. A very simple approach suggested by Allen [43] is the forward transduction model. The model scheme is drawn in Figure The input variables are the cilia force f c (effort), and velocity ξ c (flow). The output variables are the membrane voltage V m (effort), and the membrane current Q m (flow). Since the system depicted in Figure 1.12 is linear we obtain:
44 32 Figure 1.12: Allen forward transduction outer hair cell model [43]. [ Vm ] [ Af B f ] [ fc ] = (1.5.1) Q m C f D f ξ c where A f, B f, C f and D f are complex functions of frequency. This circuit depicted in figure 1.12 is analogous to a transistor. The second part of Allen s OHC model is the reverse transduction model, for which the input is the membrane voltage V m, and the current Q m, which represents the output variable of the forward transduction. The output variable is the cell movement, which may be characterized as the cell fluid volume flow ν (flow). The conjugate variable to a fluid volume flow is the turgor pressure (effort). ] ] [ ν = C r [ Ar B r D r ] [ Vm Q m (1.5.2) Given the cell turgor pressure and volume velocity, the axial force F z and the cell length change L is given by: ] ] [ Fz L = C s [ As B s D s ] [ ν (1.5.3)
45 33 Figure 1.13: A simple piezoelectric-like model of an outer hair cell from Mountain and Hubbard [21]. Allen s model [43] treats the outer hair cell as a two variable input and two variable output system. This representation was chosen since the longitudinal soma stiffness changes by at least a factor of 2 [93] as a function of cell membrane voltage, while the OHC length changes by a factor of 1.05 [90, 46, 39]. Therefore, a reasonable solution is to model both the stiffness and the elongation. Mountain and Hubbard [21], adopted the same principles employed in piezoelectric models to explain OHC operation. They assumed that the OHC voltage dependent length correlates with cell membrane potential, and the length change is associated with charge movement within the well membrane. The length changes result in voltage changes. Thus, this charge movement manifests itself as a nonlinear capacitance. The piezoelectric model of an outer hair cell is illustrated in Figure 1.13.
46 34 The piezoelectric effects represent a bi-directional coupling between the mechanical and electrical systems. In a bi-directional mechanism, the mechanical system affects the electrical impedance of the cell membrane, and visa versa. Standard models of piezoelectric devices consist of an electrical circuit representing the passive electrical characteristics of the device, coupled through a transformer to a second circuit, which is the electrical analog of the mechanical properties of the device, and its load. In the mechanical circuit, voltage corresponds to force, and current corresponds to velocity. The tension gated channels in the stereocilia produce a receptor current I A. The receptor current entering the cell must be balanced by the current leaving the cell. Some of this current represents ionic current through membrane channels G B. Some of this current leaves as a displacement current in the cell membrane capacitance C M, and the remainder exits via the transformer. This transformer current represents the charge movement associated with the cell motility. The fraction of the receptor current which is transformed into mechanical motion depends on the impedance of the mechanical circuit and the transformer ratio. If the mechanical impedance is a resonant one, then it is possible that its impedance at resonance (when viewed through the transformer) will be quite low, and most of the receptor current will be coupled into the mechanical motion. A much simpler model that attempts to explain the wide frequency range of outer hair cell operation was suggested by Dallos and Evans [68]. This model raises the issue of biological membrane cutoff frequency, and the outer hair cell operating range. On one hand, the biological membrane has a cutoff low pass filter at frequencies less then 1kHz. On the other hand, outer hair cells function in the frequency range [50, 50000]Hz. Dallos and Evans model is illustrated in Figure 1.14.
47 35 Figure 1.14: Schematic illustration of OHCs. The endolymph-facing cellular apex has an electrical impedance of Z a. The perilymph facing basolateral membrane impedance is Z b. The motility motor is symbolized by M. Shunt impedance between scala media and organ of Corti fluid is denoted by Z sh. From Dallos and Evans [68]. The OHC transducer current is produced by the modulation of Z a by means of mechanically activated transducer conductance. This modifies a standing current maintained by biological batteries embodied in the positive polarization of the endolymph and in the hair cell negative resting potential. The basolateral voltage drop operates the electromotility motor. The apical membrane impedance consists of a resistor connected in parallel to a capacitor and therefore, as the frequency is higher, its impedance is also greater. Hence, the basolateral membrane magnitude voltage drop, which is related to the division of the apical impedance and the sum of the impedances in the apical and basolateral membrane, does not change much with frequency. A model for OHC activity that couples changes in length and stiffness to transmembrane potential was suggested by Grosh et al [2]. This model emphasizes the
48 36 importance of the in vivo mechanical and electrical loading. Gorsh et al followed He and Dallos [94],assumed that the external force applied to the OHC F ohc is given by 1.5.4: ) F ohc = K ohc (V ) (L ohc L fohc (0) g (V ) (1.5.4) Where L ohc is the length of the OHC at a given voltage and force level, K ohc (V ) is the OHC stiffness under voltage clamp condition, L f ohc (0) is the free ( zero force ) length of the OHC at zero transmembrane potential difference, and g (V ) is the active force which is taken to be a function of the transmembrane potential. The Cochlear partition stiffness is assumed to be influenced by three series stiffnesses.k t - tectorial membrane, K b - basilar membrane, and K ohc (V ). A static analysis of the forces acting on the OHC, basilar membrane and tectorial membrane yields: F ohc = γδ (1.5.5) Where γ = K b K t / (K b + K t ), and δ measures the OHC length s deformation from the the stress free length l. Equations and yields: [ ] [ δ δ = l L f ohc (V ) / ( ) ] 1 + γ kohc V R R l L ohc (V R ) 1 + γ/k ohc (V ) (1.5.6) The superscript R represents resting condition. The model was compared to in vivo measurements where the influence of direct current stimulation on the acoustic impulse response of the basilar membrane was studied. According to the models assumptions, the effect of the OHC stiffness change is greater than that of the length change.
49 Types of hearing loss Hearing loss is commonly defined as elevation of sound detection threshold. It is usually accompanied by a variety of other changes in the way that sound is perceived. Even if the sounds are amplified so that they are above the threshold for detection, the perception of these sounds is usually abnormal. People with cochlear hearing loss often report that the sounds are unclear and distorted, and that it is hard to hear comfortably over a wide range of sound levels. A common complaint is the difficulty to understand speech; especially when background sounds or reverberations are present. There are several symptoms beside elevation of the threshold that are associated with hearing loss. Examples are: two tone suppression, masking, combination tones, and acoustic emission. There are several reasons for hearing loss. A conductive hearing loss is caused by reduced efficiency of sound transmission through the outer and /or middle ear. This may be caused by wax in the ear canal, damage to the eardrum by infection or trauma, damage to the ossicles in the middle ear, or fluid in the middle ear caused by infection. These result in an attenuation of the sound reaching the cochlea. Cochlear hearing loss involves damage to the structures inside the cochlea. It can arise in many ways, for example: by exposure to intense sounds or to ototoxic chemicals, by infection, and due to aging. These causes can produce a variety of types of damage to the cochlea. The damage may extend beyond the cochlea. For example, it may be at the auditory nerve and at higher centers in the auditory pathway. Hearing loss can occur through damage to structures or neural systems occurring at higher levels of the auditory system, for example in the auditory nerve or the auditory cortex. Such types of hearing loss are called retro cochlear loss.
50 38 Although hearing loss can involve structures other than the cochlea, most common damages occur within the cochlea. This is probably true for the majority of cases of hearing loss associated with ageing [9]. Four types of cochlear pathology associated with aging have been clinically recognized: sensory (hair cells), neural, strial and general [14]. Sensory loss is correlated with a loss in high frequency sensitivity, strial atrophy with loss of sensitivity at all frequencies, and neural loss with diminished word recognition. No consistent pathological correlates have been found for hearing loss that gradually increases with frequency, so those cases are placed in the general category [14]. 1.7 Physiology of the damaged cochlea Damage to any element within the inner ear can potentially affect hearing. The hair cells play a pivotal role. There is strong evidence that the inner hair cells are the principle translators of sound information, and the outer hair cells mediate collection of that information at low intensities. One of the primary lines of evidence to support the distinctions made between hair cell types is due to the investigation of damaged cochleas. Liberman and Dodds [61] exposed cat ears to a narrow band of intense noise centered at 9 khz for several hours. Almost all of the hair cells in the cat cochleas were still physically present a month later, with appreciable losses confined to a narrow region. There is strong evidence that the functioning of the normal cochlea depends upon the operation of an active mechanism that is linked to the integrity of the outer hair cells [9]. This mechanism may involve feedback of energy to the basilar membrane, via the outer hair cells. It plays an important role in producing the high sensitivity of
51 39 Figure 1.15: Hearing loss due to inner or outer hair loss [14]. the basilar membrane to weak sounds, and the sharp tuning on the basilar membrane. Cochlear hearing loss usually involves damage to the inner and outer hair cells. Figure 1.15 schematically depicts this type of hearing loss. The stereocilia may be distorted or destroyed, or entire hair cells may die. The outer hair cells are generally more vulnerable to damage than the inner hair cells. When outer hair cells are damaged, the active mechanism tends to be reduced in effectiveness or lost altogether. As a result, sensitivity to weak sounds is reduced, and the basilar membrane responses are much more broadly tuned. The effects of cochlear damage on the input output function were demonstrated by Ruggero and Rich [58]. They injected furosemide into the cochlea, and demonstrated loss of sensitivity and loss of nonlinear relationship between stapes velocity and basilar
52 40 membrane velocity at the characteristic frequency region. The furosemide causes dysfunction the outer hair cell activity. 1.8 Motivation of the present study Cochlear hearing loss usually involves damage to the inner and outer hair cells. The outer hair cells are generally more vulnerable to damage than the inner hair cells. When outer hair cells are damaged, the active mechanism tends to be reduced in effectiveness or lost altogether. As a result, sensitivity to weak sounds is reduced, and the basilar membrane responses are much more broadly tuned. Modeling is a potential shortcut to understanding how the cochlea works. Computational modeling of the cochlea can help to validate hypotheses, interpret data and buttress the basis of the conceptual model. The major effort of this present thesis is to explain the outer hair cell contribution to hearing by means of a basic model. We seek to develop a tool that can test physiological and psychological phenomena. The model should be bio-physical and macro-mechanical. Much criticism has been made of the one dimensional approach to modeling the cochlear fluid dynamics [37, 22]. However, the one-dimensional model is the simplest to understand and to implement as a computational model. The motivation for this study was these simple biological based models of the OHC. As we know the essential role of OHC in hearing, the incorporation of a OHC model in a one-dimensional cochlear model might predict phenomena of normal and impaired hearing.
53 Chapter 2 The Model Description 2.1 Introduction The model presented in this thesis is a one-dimensional cochlear model with embedded outer hair cell model. The embedded model is analyzed for very small stimulation magnitudes where it can be treated as a linear model. Methods to solve this problem are discussed, including the WKB and the finite difference method. For moderate magnitude stimuli, this embedded model cannot be treated as linear; therefore a time dependent solution algorithm is proposed and analyzed. 2.2 Cochlear Fluid Dynamics In the simple one-dimensional model Zwislocki [48]; Zweig et al [32]; Viergever [60] Furst and Goldstein [57], the cochlea is considered as an uncoiled structure with two fluid-filled rigid-walled compartments separated by an elastic partition. In the proposed model we shall include the OHC activity in the elastic partition. The basic equations are obtained by applying fundamental physical principles such as conservation of mass and the dynamics of deformable bodies. The cochlear model used in this study contains an outer hair cell model. The outer 41
54 42 Figure 2.1: Cochlear model geometry hair cell model is embedded in the one dimensional cochlear model. These two models control each other through cochlear partition movement and cochlear partition cross pressure variables. If we assume that the cochlea is uncoiled and approximated by two fluid-filled rigid-walled compartments separated by an elastic partition, then it may be represented by a one-dimensional model as shown in Figure 2.1. In order to arrive at a mathematically tractable model, simplifying assumptions are required. An extensive mathematical one-dimensional cochlear model can be found in [60]. Let x be the longitudinal coordinate such that at the basal end x = 0 and at the apical end x = l where l is the uncoiled cochlea length. Let t be the time variable. Let P v (x, t) be the pressure through scala vestibuli and P t (x, t) is the pressure through scala tympani. The intermediate channel between the scala vestibuli and the scala tympani is
55 43 called the scala media and is represented by the elastic partition. The vertical displacement of the partition along the x dimension is denoted ξ bm (x, t). The fluid velocity along the x dimension is U v (x, t) and U t (x, t) for the scala vestibuli and the scala tympani, respectively. The principle of conservation of mass yields the equations: A U v x β ξ bm t = 0 (2.2.1) A U t x + β ξ bm t = 0 (2.2.2) where β(x) is the basilar membrane width and A(x) is the scalae cross section area. Since both scalae tympani and vestibuli contain perilymph, which we can assume is an almost incompressible and inviscid fluid, the equation of motion for each scala can be written as: P v x + ρ U v t = 0 (2.2.3) where ρ is the perilymph density. P t x + ρ U t t = 0 (2.2.4) This set of equations is completed by the equation of motion of the cochlear partition. framework. The partition is, mechanically, a flexible structure embedded in a rigid It is assumed that the flexible part, the basilar membrane, and the structure above it have point wise mechanical properties. This means that the velocity at any point of the partition is related to the pressure difference across the partition at that point only and not at neighboring points.
56 44 We define the pressure difference across the cochlear partition as: P = P t P v (2.2.5) The cochlear partition is regarded as a flexible boundary between scala tympani and scala vestibuli, whose mechanical properties are describable in terms of point-wise mass density, stiffness and damping. Thus, at every point along the cochlear duct, the partition s velocity is driven by the pressure difference P across the partition. From the principle of conservation of mass we can derive the relationship between the fluid velocity and the basilar membrane displacement ξ bm Combining equations, Eq Eq 2.2.5, yields the differential equation for P : 2 P x 2ρβ(x) 2 A Assume the following boundary conditions: 2 ξ bm t 2 = 0 (2.2.6) U v (0, t) = U t (0, t) = S(t) (2.2.7) P (l, t) = 0 (2.2.8) where S(t) is the stapes velocity, and l is the cochlear length. These boundary conditions, together with Eq: and 2.2.3,yield more convenient boundary conditions: t 0 P x = 2ρdS(t) dt P (x, t) = 0 x = 0 (2.2.9) x = l
57 45 Assume that the cochlea stimuli started from the rest condition, then the initial value conditions are: x [0, l] ξ bm (x, 0) = 0 (2.2.10) ξ bm (x, 0) = 0 dt In previous one-dimensional cochlear models, Zwislocki [48], Viergever [60], Furst and Goldstein [57], the pressure difference is only obtained by the basilar membrane mechanical properties. In this model, we include the pressure produced by the OHCs P ohc, therefore: P bm = P + P ohc (2.2.11) where: P bm (x, t) = m(x) 2 ξ bm 2 t + r(x, t) ξ bm t + s(x, t)ξ bm (2.2.12) where m(x), r(x, t) and s(x, t) represent the basilar membrane mass, resistance, and stiffness per unit area (length), respectively. Since the basilar membrane motion of a passive cochlea is limited and reaches saturation, we assume that the resistance and stiffness of the passive basilar membrane are functions of the basilar membrane motion and therefore can be regarded as functions of time. The outer hair cell model and the corresponding equations for P ohc are presented in the next section. According to Furst and Goldstein [57], it is reasonable to assume that the damping factor r(x, t) and the stiffness are given by:
58 46 r(x, t) = r 0 (x)(1 + ɛ 1 [ dξ bm dt (x, t)]2 ) (2.2.13) where r 0, ɛ 1, s 0, ɛ 2, δ are constants. s(x, t) = s 0 (x)(1 + ɛ 2 ξ δ bm(x, t)) (2.2.14) 2.3 The Outer Hair Cell Model OHC Mechano - Electrical model The object of this section is to obtain an OHC model which will explain the OHC operation at all audible frequencies. Since the basolateral membrane electrical analog is a low-pass filter, the apical membrane model contribution will yield an all-pass filter configuration. Dallos and Evans [68] proposed that electro-motility at high frequencies is obtained by extracellular potential gradient across the hair cell. They proposed that the outer hair cells are partitioned in vivo between two fluid compartments. The cell membrane is divided into two parts, the apical part facing scala media and the basolateral part embedded in organ of Corti. These two cell membrane segments are represented as two parallel resistance and capacitance circuits. The following model is a modification of the above proposal. Assumptions are made to yield an all-pass filter configuration that can explain the OHC wide band frequencies operation range. In order to maintain compatibility with other models [26], we introduce a battery in series with the basolateral membrane resistor. This battery is for the equivalent electrochemical gradient across basolateral membrane. Figure 2.2 represents an equivalent electrical circuit model for the OHC.
59 47 G a Ca ψ V sm G b ψ 0 C b Figure 2.2: An equivalent electrical circuit of the outer-hair cell We assume that both the capacitance and conductance (of the apical part) are affected by the stereocilia movement. The electrical potential across the cell membrane is assumed equal to the potential of the scala media V sm, and the potential difference across the basolateral part (the receptor potential) is presented by ψ, c.f. Figure 2.2. The stereocilia motion causes a current flow through the apical part of the OHC which yields apical current I a. The electrical impedances of the two cell membrane segments facing endolymph and perilymph respectively, are represented as a two resistor capacitor circuit. Therefore the current flow through the basolateral membrane is I b : I b = G b (ψ ψ 0 ) + C bd(ψ) dt = C b dψ dt + ψ dc b dt + G b(ψ ψ 0 ) (2.3.1) where C b, G b are the basolateral membrane capacitance and conductance respectively and, ψ, ψ 0 and are the basolateral membrane capacitance, voltage drop, equivalent electrochemical gradient, and conductance respectively. The current flow trough the apical membrane is I a : I a = C a d(v sm ψ) dt + (V sm ψ) dc a dt + G a(v sm ψ) (2.3.2)
60 48 Where C a, and G a, are the apical membrane capacitance and conductance. In accordance with Kirchhoff s current law, the current that flows through the apical segment is equal to the current that flows through the basolateral segment. Thus I a = I b yields the differential equation for ψ: C a dv sm dt + V sm ( dc a dt + G a) + G b ψ 0 = (C a + C b ) dψ dt + (dc a dt + dc b dt + G a + G b )ψ (2.3.3) In order to simplify Eq: 2.3.3, we apply the following assumptions: 1. The capacitance and the conductance of the OHC s membrane are proportional to the membrane surface area. The basolateral membrane area is larger than the apical part. According to Housley and Ashmore [33] the ratio between the basolateral and apical capacitance is more than sixteen, and the ratio of the conductance is more than seven. We thus assume G a G b and C a C b. 2. The changes in the basolateral capacitance are relatively small, thus dc b dt = 0 (2.3.4) 3. We shall further assume that G a and dc a /dt are of the same order of magnitude. 4. The electrical potential across the scala media is assumed constant (Mountain and Hubbard [26]), thus dv sm dt = 0 (2.3.5) Thus, from 1 and 3 we can conclude that dc a dt G b (2.3.6)
61 49 G a Ca ψ V sm G b ψ 0 C b Figure 2.3: simplified OHC s electrical circuit model. Based on figure 2.2 and incorporating assumptions 1-4 The OHC membrane acts as a low-pass filter with a cutoff frequency less then 1 khz, Dallos and Evans [68]. We define the OHC s cutoff frequency ω ohc as: ω ohc = G a + G b C a + C b G b C b = const (2.3.7) Substituting equations, Eq: Eq into equation Eq: yields a simplified differential equation for ψ : where: dψ dt + ω ohcψ = λ( dc a dt + G a) + ω ohc ψ 0. (2.3.8) λ = The simplified OHC s model is shown in Figure 2.3. V sm C b + C a V sm C b (2.3.9) OHC Apical Membrane Electrical Principle Variations The apical membrane capacitance and conductance undergo changes due to active opening of ion channels in the apical part of the outer hair cell. The outer hair
62 50 cell stereocilia are shallowly but firmly embedded in the under-surface of the tectorial membrane. Since the tectorial membrane is attached on one side to the basilar membrane, a shear motion arises between the tectorial membrane and the organ of Corti as the basilar membrane moves up and down (Pickles [52]). The arch of Corti maintains the rigidity of the organ during the movement. For simplicity, we further assume that the tectorial membrane, along with the Dieters cells, is a rigid structure. Thus, it is reasonable to assume that the outer hair cell bundle displacement is a function of the basilar membrane vertical displacement, (Nobili et al [74]). Therefore, both G a and C a are functions of ξ bm (the basilar membrane vertical displacement). The hair bundle displacement is a result of opening and closing of the ion gates. It is also generally accepted that the transduction channels are opened via elastic elements, called gating springs. Their functional dependence is best described by a second order Boltzmann function (e.g. Sachs and Lecar [29]; Lukashkin and Russel [7]). The mechano-electrical transducer of the hair cell is an early, crucial stage in auditory sensory processing with strong non-linear characteristics. This non-linear relationship between hair bundle displacement and transducer conductance has been fitted for cochlea in mice by a second-order Boltzmann (three-state model) function, [26]. This function describes the probability of a transducer channel opening to the displacement of the hair bundle. Therefore the conductance of the apical segment G a is given by: G a = G k 2 (1 + k 1 ) (2.3.10) k 1 is the equilibrium constant between the open state and the first closed state. k 2
63 51 is the equilibrium constant between the two closed states. k 1 and k 2 can be described in terms of the position of the hair bundle: k 1 = exp(α 1 [η 1 ξ b ]) (2.3.11) k 2 = exp(α 2 [η 2 ξ b ]) where α 1, α 2, η 1, η 2 are constants and ξ b is the displacement of the hair bundle from the resting point (Mountain and Hubbard [26] Lukashkin and Russell [27]). Figure 2.4 represents the conductance G a as a function of the hair bundle displacement ξ b. The graph in Figure 2.4 was obtained by Eq: and Eq: , with the following parameters: α 1 = nm, α 2 = nm, η 1 = 24 nm and η 2 = 41 nm. The tip of the hairs of the outer hair cells have been reported to be firmly embedded in the under-surface of the tectorial membrane. The tectorial membrane is attached only on one side and is raised above the basilar membrane. Therefore, when the basilar membrane moves up and down, a shear, or relative movement, will occur between the tectorial membrane and the organ of Corti [52]. The arch of the pillar cells (the arch of Corti) would seem well suited to maintain the rigidity of the organ of Corti during such a movement. The tectorial membrane is also a rigid structure; thus, it is reasonable to assume that the outer hair cell bundle displacement is some homogenous function of basilar membrane vertical displacement. For mathematical brevity, we assume that ξ b = ξ bm. Where ξ bm is the cochlear partition vertical displacement. Therefore, equation is written:
64 conductance [ns] displacement [nm] Figure 2.4: Transducer conductance of the mammalian outer hair cell as a function of bundle displacement. k 1 = exp(α 1 [η 1 ξ bm ]) (2.3.12) k 2 = exp(α 2 [η 2 ξ bm ]) In vivo, for non stimulated cochlea, every hair cell bundle has its own resting deflection. This deflection is assumed to adjust the working point of the OHC amplifier. Assuming that the resting point is close to the maximum sensitivity point and the hair bundle displacement is relatively small, then Eq can be approximated by a linear equation which yields: G a (ξ b ) = α g ξ b + α 0 g (2.3.13) where α g and α 0 g are sensitivity and offset positive constants. This linear approximation with the basolateral resistor capacitor circuit cannot explain the wide range of frequencies that mammals are able to hear. Even by adding a
65 53 constant capacitor element to the apical membrane circuit model, the high frequencies gain is not explained; therefore, it is assumed that the apical membrane capacitance is also a linear function of the bundle displacement ξ b. The apical membrane capacitance linear approximation is given by: C a (ξ b ) = α c ξ b + αc 0 (2.3.14) where α c and αc 0 are sensitivity and offset positive constants. Substituting Eq: and Eq: in Eq:2.3.8 with the assumption that the hair bundle displacement is equal to the basilar membrane displacement i.e. ξ b = ξ bm yields: term. dψ dt + ω dξ bm ohcψ = λ(α c + α g ξ bm ) + (λαg 0 + ω ohc ψ 0 ). (2.3.15) dt The last equation resembles an all-pass filter configuration with an extra additive Regulated Current Source The outer hair cell electrical model can be approached from another aspect and a very similar mathematical expression obtained as in Eq: Let us assume that the ion current into the hair cell is controlled by both the bundle displacement ξ b and by the bundle velocity dξ b /dt. The assumptions are similar to those used earlier, i.e: 1. The basolateral membrane capacitance and resistance are time invariant. 2. The current flow through the basolateral membrane is regulated by a linear combination of basilar membrane displacement and velocity.
66 54 I a ψ G b ψ 0 C b Figure 2.5: Alternative Electrical circuit representing an outer hair cell in vivo. The current source is a function of bundle displacement and velocity. 3. The basilar membrane displacement equals the bundle displacement ξ b = ξ bm. Figure 2.5 depicts the model s electric circuit, where G b, C b I a, ψ are the cell basolateral membrane electrical conductances, capacitance, current flow, and voltage drop across the cell, respectively. As before ψ 0 is the basolateral equivalent battery. The current source is regulated by a combination of basilar membrane displacement and velocity. This current source can be modulated by a variety of mechanisms. For example, by the cilia motion which may be controlled by the mechanical properties of the hair bundle, or by the fluid motion between reticular lamina and tectorial membrane, etc. Applying assumptions 2, and 3, reveals that the cell input current I a is given by: where d 2, d 1, d 0 are constants. I a = d 2 ξ bm dt + d 1ξ bm + d 0 (2.3.16) In accordance with Kirchhoff s current law, the current flow through the apical segment is equal to the current flow through the basolateral segment: I a = (ψ ψ 0 )G b + d dt (ψc b) (2.3.17)
67 55 Substituting Eq in Eq with assumption 1 yields: dψ dt + ω ohcψ = 1 C b (d 2 ξ bm dt + d 1ξ bm ) + ω ohc ψ 0 + d 0 C b. (2.3.18) Where ω ohc = G b /C b as in Eq: Eq: is similar to Eq: if we call : d 0 = V sm α 0 g d 1 = V sm α g d 2 = V sm α c (2.3.19) When considering the outer hair cell functionality as a system that has basilar membrane displacement as an input and produces force as an output, the simplest way to explain its operating frequency range is by an all-pass filter configuration. For this reason, the basilar membrane displacement and the velocity control the voltage drop in the first and second outer hair models. In the first model this is achieved by variable conductance and capacitance, and directly by current source control in the second model. We have shown that mathematically we cannot distinguish between those two approaches Voltage Dependent Length Cochlear outer hair cells are sensory receptor cells that have motor capability. The membrane potential-dependent motor process is said to provide mechanical feedback to the basilar membrane-tectorial membrane complex of the cochlea [90, 46, 40]. Changes in an outer hair cell length are controlled by the voltage change across the
68 56 outer hair cell basolateral membrane ψ. Santos-Sacchi [38] demonstrated that the length change could be predicted by a two-state Boltzmann distribution. Dallos, Hallworth, and Evans [69] extended this idea by proposing a model for the voltagesensitive proteins that is similar to those used for voltage-dependent ion channels, as was discussed in the previous section. They suggested that these proteins have two stable states in space (short and long). In their model, the transitions between the two states is a stochastic function of membrane potential represented by a second-order Boltzmann process. Let us assume that the OHC is bound between the basilar membrane and the tectorial membrane as shown in Figure 2.6. The distance between the basilar membrane and the tectorial membrane is conserved, so it is called the isometric model. This isometric model is based on previous OHC model, suggested by Dallos and He [93]. Let us assume that the OHC is loaded in both sides, between the basilar membrane and the tectorial membrane, and the following assumptions are considered: 1. The distance between basilar membrane and tectorial membrane is constant and ξ 0 = The tectorial stiffness K 0 is assumed to approach infinity relatively to the OHC stiffness [2]i.e.(K 0 K ohc ). The equilibrium of forces c.f. Figure 2.6 is given by: K ohc ( l ohc (ψ) + ξ bm x) = K 0 (x ξ 0 ) (2.3.20) where K ohc is the OHC stiffness, K 0 is the load stiffness, l ohc (ψ) is the unloaded (open circuit) motile response, ξ bm is the basilar membrane displacement, ξ 0 is the
69 57 ξ bm l ohc K ohc K 0 x ξ 0 Figure 2.6: The motile OHC is loaded by a constant stiffness K 0, It delivers a force F ohc to the load. ξ bm is the partition displacement. load length change and x is the displacement between the OHC and the load. F ohc represents the force that an OHC exhibits in response to voltage change. From Eq: we get : Substituting assumption 1 yields : x = ( l ohc(ψ) + ξ bm )K ohc K ohc + K 0 + ξ 0K 0 K ohc + K 0 (2.3.21) From Hook s law, F ohc = xk 0, we obtain: x = ( l ohc(ψ) + ξ bm )K ohc (ψ) K ohc + K 0 (2.3.22) Substituting assumption 2 yields : F ohc = ( l ohc (ψ) + ξ bm ) K ohck 0 K ohc + K 0 (2.3.23) F ohc = K ohc ( l ohc (ψ) + ξ bm ) (2.3.24) Assumption 2 leads us to a simpler model;a model of a spring loaded in one side. In the one side loaded spring model, the OHC s elongation is the sum of basilar membrane motion and the OHC s length change due to basolateral voltage drop.
70 58 Force [nn] command voltage [mv] Figure 2.7: OHC s isometric force (from He and Dallos [93]) Where l ohc is a function of the voltage drop across the basolateral membrane which resembles a Boltzmann distribution function [38, 93], c.f. Figure 2.7. The spring stiffness K ohc is a constant. For low level stimuli we assume that the OHC length change is given by: l ohc = α 0 l α l ψ (2.3.25) where α 0 l and α l are positive constants. There are many OHC per unit area, therefore the pressure applied by these OHCs on the cochlear partition is given by: P ohc = γ(x)f ohc (2.3.26) where γ(x) is the relative density of healthy OHCs per unit area (length) along the cochlear duct. We will refer to γ(x) as the OHC gain, whose value ranges from 0 to 1.
71 OHC Pressure Contribution In this section we calculate the OHC s pressure contribution P ohc due to partition vertical displacement ξ bm. From Eq: we get: dp ohc dt + ω ohc P ohc = γ(x) df ohc dt Substituting equation Eq: in Eq: yields: + ω ohc γ(x) F ohc (2.3.27) dp ohc dt + ω ohc P ohc = γ(x)k ohc [ d[ξbm + l ohc (ψ(ξ bm ))] dt + ω ohc [ ξbm + l ohc (ψ(ξ bm )) ]] = γ(x)k ohc [ dξbm dt + ω ohc ξ bm part 1 {}}{ ] d l ohc (ψ(ξ bm )) + + ω ohc l ohc (ψ(ξ bm )) dt (2.3.28) Considering part 1 in the above equation and substituting Eq: yields: d l ohc (ψ(ξ bm )) dt + ω ohc l ohc (ψ(ξ bm )) = d[α0 l α lψ] + ω ohc (αl 0 α l ψ) dt part 2 {}}{ = α l ( dψ dt + ω ohcψ) +ω ohc α 0 l (2.3.29) Substituting Eq: for part 2 in the above equation, and after some further manipulation, yields:
72 60 d l ohc (ψ(ξ bm )) dt +ω ohc l ohc (ψ(ξ bm )) = α l (λ[α 0 g +α g ξ bm +α c dξ bm dt ]+ω ohcψ 0 )+ω ohc α 0 l (2.3.30) which after substituting the manipulated part 1 back and some minor rearrangement can be written: dp ohc dt [ ] dξ bm + ω ohc P ohc = γ(x) α 2 + α 1 ξ bm + α 0 dt (2.3.31) where α 0, α 1, α 2 are as follows: α 2 = K ohc [1 λα l α c ] α 1 = K ohc [ω ohc λα l α g ] α 0 = K ohc [ ωohc α 0 l λα l α 0 g α l ω ohc ψ 0 ] (2.3.32) Eq: is linear hence we can separate it into two components, and as ξ bm is a function of t we can write it in general : dp ohc dt + ω ohc P ohc = f(ξ bm, ξ bm) + Const P ohc = P (1) ohc + P (2) ohc where f(ξ bm, ξ bm (2) ) is in general a function of t and P ohc obeys : and therefore: dp (2) ohc + ω ohc P (2) ohc dt = Const P (2) ohc = Ce ω ohct + Const
73 61 This solution will converge into a constant, and therefore will not contribute to the amplification of the alternate signal. Hence Eq: is reduced to: dp ohc dt [ ] dξ bm + ω ohc P ohc = γ(x) α 2 + α 1 ξ bm dt (2.3.33) In order to solve Eq: , all the parameters should be determined. However, it is easier to obtain the values of α 1 and α 2 by using the frequency domain solution. For a steady state sinusoidal input, the frequency domain representation of Eq: is given by: where j = 1. P ohc (x, ω) = γ(x)ξ bm (x, ω) α 1(x) + jωα 2 (x) ω ohc + jω (2.3.34) Substituting Eq: in the frequency domain representation of Eq: : P bm = P + P ohc Now, we assume linearity; hence Equation is as follows: P bm (x) = m(x) 2 ξ bm 2 t + r(x) ξ bm t + s(x)ξ bm which yields: P = P bm P ohc = [ P (x, ω) = ξ bm (x, ω) m(x)ω 2 + jr(x)ω + s(x) γ(x) α ] 1(x) + jωα 2 (x) ω ohc + jω We can, for simplicity, write it as: P (x, ω) = Ϝ(x, ω)ξ bm (x, ω) (2.3.35) where:
74 62 Re(Ϝ(x, ω)) = m(x)ω 2 + s(x) γ(x) α 1(x)ω ohc + α 2 (x)ω 2 ω 2 + ωohc 2 Im(Ϝ(x, ω)) = r(x)ω γ(x)ω α 2(x)ω ohc α 1 (x) ω 2 + ωohc 2 (2.3.36) We further assume that a resonance is produced for every location along the cochlear partition when the stimulus frequency ω is equal to s(x) ω cf (x) = m(x) The resonance frequency in a cochlea with no active OHCs γ(x) 0, is obtained when Re(Ϝ(x, ω cf )) = 0, but Im(Ϝ(x, ω cf )) 0. When γ(x) 1, we require that at the resonance frequency both Re(Ϝ(x, ω cf )) = 0, and Im(Ϝ(x, ω cf )) = 0. Substituting these requirements in Eq: reveals the values for α 1 (x) and α 2 (x): α 1 (x) = r(x)s(x) m(x) (2.3.37) α 2 (x) = r(x)ω ohc (2.3.38) Comparison between these equations and the ones from the variable length model constants: α 2 = K ohc [1 λα l α c ] α 1 = K ohc [ω ohc λα l α g ] (2.3.39) yields some constraints on the parameters α g, α c and α l ; specifically:
75 63 λα l α g > ω ohc (2.3.40) and: λα l α c < 1 (2.3.41) This implies that α c < α g /ω ohc. This result might explain why changes in the OHC s apical conductance were more frequently detected than its capacitance changes. Moreover, since the characteristic frequency ω cf changes relatively quickly along the cochlear partition in comparison to the basilar membrane resistance r(x) (Table: 6.1), we can conclude that α g changes significantly along the cochlear partition, while α c changes relatively slowly.
76 Chapter 3 Frequency Domain Solution 3.1 Frequency Domain Formulation A linear version of the model was developed in the previous chapter. It is natural to seek a solution for this linear model in the frequency domain. Transforming Eq: into the frequency domain yields: 2 P (ω) x 2 + ω 2 2ρβ A ξ bm(ω) = 0 (3.1.1) The transformation of Eq into frequency domain gives: P bm (ω) = ( ω 2 m + jωr + s)ξ bm (ω) (3.1.2) and for Eq : [ ] jωα2 + α 1 P ohc (ω) = γ(x)ξ bm (ω) jω + ω ohc (3.1.3) These three equations can be combined into one using: Eq : P = P bm P ohc and Eq : P (x, ω) = Ϝ(x, ω)ξ bm (x, ω): 2 P (ω) + ω 2 2ρβ P (ω) = 0 (3.1.4) x 2 AϜ(ω) 64
77 65 The function: Ϝ(ω) was defined in The impedance function Z(ω) was defined as Z(ω) = P (ω)/(jω ξ bm (ω)). Hence: Ϝ(ω) = Z(ω)jω (3.1.5) Since we consider the cochlea as a system having stapes velocity as input and basilar membrane displacement as output, it is convenient to normalize the amplitude of the stapes motion to one unit of velocity (i.e.,1 µm ). Since the system is linear, this can Sec be done without loss of generality. Thus, by Eq: and equations: 2.2.3, the boundary condition at x = 0 t reads: P x x=0 = 2ρ ds dt and by transform into the frequency domain we have: U v (0, t) = e jωt P (ω) x x=0 = 2jωρS(ω) (3.1.6) The second boundary condition, at the apical end is found by Eq: , the boundary condition at x = l for all t reads: P (ω) x=l = 0 (3.1.7) Wave Number Function Representation The solution of the one-dimensional model equation may be obtained either directly by numerical means or in an approximative manner by applying an asymptotic technique.
78 66 If ω is considered constant then Eq: 3.1.4, 3.1.5, Eq: and Eq reduce to an ordinary differential equation (in x ) subjected to two boundary conditions. The boundary value problem is written: d 2 P dx 2 + K2 P = 0 (3.1.8) where K 2 is: K 2 (x) = 2jωρβ AZ(x) and the boundary conditions from Eq: 3.1.6and Eq: are written by: (3.1.9) dp dx x=0 = 2jωρS(ω) P x=l = 0 (3.1.10) where K(x, ω), P (x, ω), and ξ bm (x, ω) are the wave number function, the pressure, and the partition vertical displacement along the partition respectively. For constant K Eq: is reduced to Helmholtz equation Finite Difference Solution The finite differences method is one of the simplest methods to solve this boundary value conditions problem. Although the finite elements methods gives a better approximation, numerical computation using the finite differences method for a dense net is easier. The main principle of the finite difference method is to substitute derivatives appearing in the differential equation with numerical approximations of these derivatives. The derivatives approximation is a weighting sum of the solution function on
79 67 net point. The result of that substitution is that the derivatives are replaced by relationships between the function values at nodal points of some net. Hence the differential equation is approximated by a set of algebraic equations for the function values at the nodal points. In order to transform to the discreet representation, expressions such as dp dx and d 2 P (3.1.11) dx 2 at typical grid points are required in terms of the P values at neighboring net points. On the interval[0, l] we place a uniform net, say: x j = jh h = l N j = 0, 1,, N (3.1.12) Since all the functions henceforth are of ω we shall dispense with the noting of it. Using a linear combination of Taylor series at x = x i for P i 1 and P i+1,at each interior net point, x j j = 1, 2,, N 1 gives ( ) d 2 P = P j 1 2P j + P j+1 + O(h 2 ) (3.1.13) dx 2 x=x j h 2 Similarly, at the exterior points, Taylor series gives: ( d 2 P dx 2 where P j = P (x j ) and P j = (dp/dx)(x j ). )x=x0 = 2(P 1 P 0 hp 0) h 2 + O(h) (3.1.14) In order to approximate P (x, ω) on this net, we define a net function {u j } as the solution of the system of finite difference equations which are in some sense an approximation to the boundary problem given above. Eq:
80 68 At each interior net point, x j j = 1, 2,, N 1, Eq: is replaced by corresponding centered difference quotients to give u j 1 (2 h 2 Kj 2 )u j + u j+1 = 0 (3.1.15) where Kj 2 = K 2 (x j ). At interior points we can approximate derivatives to O(h 2 ) by using two neighboring points. For exterior net points, approximation is somewhat more complicated since one of the neighbors is missing. We expect the function to be very smooth at the edges since we limit the range of the stimulus frequencies from 200Hz to 15kHz and it is far from the characteristic frequency of the edges, and therefore the O(h) approximation is good enough at the edges. It is possible to have better approximation by taking linear combinations of more points, but this is not necessary. Instead, substituting approximations in equation 3.1.4, gives u 1 (1 h 2 K2 0 2 )u 0 = hp 0 = h2jρωs(ω) (3.1.16) P N = 0 (3.1.17) The last three equations, Eq: , Eq: and Eq: combine into a linear system. Au = r (3.1.18) where we have introduced the N + 1 dimensional vectors:
81 69 u = u 0 u 1. u N 1 u N r = h2jωρs(ω) (3.1.19) and the N + 1 order matrix is written: A = (1 h 2 K0 2 2 ) 1 1 (2 h 2 K1) (2 h 2 K 2 N 1 ) (3.1.20) In this way, if matrix A is regular, then a unique solution exists and easily obtained. Matrix A regularity for every K(x) and for every positive h is questionable. But if an inverse matrix is found for a particular simulation, then we can be sure that the method works for that particular simulation. Another approach to solve the frequency domain model is by using the WKB approximation, as described in the following section The Liouville Green Approximation A well known solution to the frequency domain problem is by using the Liouville Green method [32, 60]. The solution of equation Eq: with constant K 2, implied on the substitution: P (x) = e jϕ(x) (3.1.21)
82 70 Therefore d 2 P dx 2 ( [ ] ) 2 dϕ = jp j + d2 ϕ dx dx 2 Assume that x : P 0 otherwise the boundary condition must be zero. Thus Eq: becomes : (3.1.22) ( ) 2 dϕ + j d2 ϕ dx dx + 2 K2 = 0 (3.1.23) If d 2 ϕ/dx 2 is assumed small, a first approximation gives to yield the first approximation ( ) 2 dϕ = K 2 (3.1.24) dx ϕ(x) = ± x 0 K(ν)dν + ϕ(0) (3.1.25) As we assumed without loss of generality that P (0) = 1,we deduced that ϕ(0) = 0 by Eq: The condition of validity gives d 2 ϕ dx 2 K 2 dk dx K 2 (3.1.26) A second approximation is found by an iteration. The first approximation set d 2 ϕ/dx 2 = 0. The first approximation gave dϕ/dx = ±K. So we suggest the substitution of d 2 ϕ dx = ±dk 2 dx (3.1.27) in Eq: Hence we read
83 71 ( ) 2 dϕ ±j dk dx dx + K2 (3.1.28) By taking the first term in Taylor series of the square root function, the approximation becomes: since by Taylor series we get : dϕ dx ±K + j dk 2K dx (3.1.29) K2 ) ± jdk/dx K 2 ± jdk/dx 2 = ±K ± jdk/dx K 2 ±2K and the corresponding solutions approximation ϕ(x) ± x 0 K(ν)dν + j ln K(x) (3.1.30) 2 Higher order approximations may be obtained by further iterations. It is customary, however, to use the above approximation. The two choices of sign gives the combined Liouville Green solution. ( P (x) AK(x) 0.5 exp j x 0 ) ( K(ν)dν + BK(x) 0.5 exp j x 0 ) K(ν)dν (3.1.31) Now, from the boundary condition P (l) = 0 we get: ( AK(l) 0.5 exp j ( l exp j K(ν)dν 0 l 0 ) ( K(ν)dν + BK(l) 0.5 exp j ) K(l) 0.5 [ A exp ( 2j l 0 l 0 K(ν)dν ) K(ν)dν ) ] + B = 0 = 0 (3.1.32)
84 72 Since the wave across the basilar membrane propagates towards the epical end, until K(x) develops a large negative imaginary part and by Eq: the wave is cutoff. The cutoff point depends monotonically on the angular frequency ω and we have: ( exp j l 0 ( B = A exp 2j ) K(ν)dν K(l) l 0 ) K(ν)dν (3.1.33) The second term in Eq: describes the wave that originated by reflection of the first wave at x = l. It is significant only for very low frequencies, where the pressure drop across the membrane at x = l has a significant value. In other words, the reflected wave is negligible when: ( j exp l Therefore from Eq: we get B = 0. 0 K(ν)dν) 1 (3.1.34) Now, from the second boundary condition dp/dx x=0 = 2jωρ and from Eq: Eq: we have: ( K 2 (x) exp dp dx x=0 = 0.5AK 0.5 (x) dk/dx = jak 0.5 (x)exp = jak 0.5 (0) = 2jωρ ( j x 0 j x 0 K(ν)dν ) K(ν)dν ) x=0 (3.1.35)
85 73 A = 2ωρ (3.1.36) K 0.5 (0) Thus an approximation to the exact solution of Eq: has been found in any region where the condition of validity holds. The method fails if K(x) changes too rapidly or if K(x) pass through zero. When the extreme low frequencies are excluded, the solution takes a simple form once we substitute Eq: and B = 0 in Eq: which yields: 2ωρ P (x) K 0.5 (0)K 0.5 (x) exp ( j x 0 ) K(ν)dν (3.1.37) Liouville Green Vs. Finite Difference One of the assumptions made in the Liouville Green method was the condition of validity Eq: This condition is not valid. The Liouville Green solution does not fulfill the condition of validity as we can see in Figure 3.1. The condition of validity Eq: is computed for γ = 0.5 and frequency = 1000 khz, the ratio between dk and K approaches 0.75 at the location of the characteristic frequency and we dx supposed to approach zero. We get very similar results for other frequencies and other cochlea parameters. As γ increases the ratio between dk and K increases as well. dx Nevertheless, great similarity is revealed when we compare the Liouville Green and the finite difference solutions. The difference between these solutions is located in the region of characteristic frequency. Figure 3.2 depicts comparison between these solutions in large scale. A closer view in the region of the characteristic frequency reveals 2.5 db difference, as shown in Figure 3.3. We can obtain a much more accurate result using a method based on the finite
86 Figure 3.1: Condition of validity for the Liouville Green solution Eq: the ratio is computed by using γ = 0.5 and frequency=1000 Hz. 74
87 Figure 3.2: Basilar membrane velocity for γ = 0.5 and frequency = 1000 Hz by Liouville Green solution and finite differences solution. 75
88 Figure 3.3: Basilar membrane velocity for γ = 0.5 and frequency = 1000 Hz by Liouville Green solution and finite differences solution. 76
89 77 differences by implementing the Richardson [80] method for approximating the second derivative using additional nodal points. It is not necessary to implement it on all nodal points; instead, we can increase the derivative s approximation order only for those nodal points close to the characteristic frequency region.
90 Chapter 4 Time Domain Solution 4.1 Mathematical Preface For the time domain solution, we rewrite the model equations in order to make them adequate to both linear and nonlinear formulations. There are two types of nonlinearity that are included in the model. The first one is cochlear partition nonlinearity i.e., Eq: and Eq: The second one is OHC nonlinearity i.e., Eq: and Eq: The OHC nonlinearities involve Boltzmann distribution functions. We suggest some functional approximation by taking a sigmoid function f nl as approximation to Boltzmann function.we rewrite Eq: : dp ohc dt [ ] dξ bm + ω ohc P ohc = γ(x) α 2 + α 1 ξ bm dt as: dp ohc dt + ω ohc P ohc = γ(x)f nl (α 2 dξ bm dt + α 1 ξ bm ) (4.1.1) where f nl is a sigmoid function, which represents the OHC nonlinearity. Eq: is subject to the initial conditions x P ohc (x, 0) = 0. 78
91 79 From Eq: P bm = P + P ohc and Eq: : m(x) 2 ξ bm 2 t + r(x, t) ξ bm t + s(x, t)ξ bm = P + P ohc (4.1.2) where r(x, t) and s(x, t) are nonlinear terms given by Eq: , and Eq: respectively. Eq: is subject to the following initial values: x [0, l] ξ bm (x, 0) = 0 ξ bm (x, 0) = 0 t Assign the symbol v bm to the partition velocity, i.e., v bm = ξ bm t (4.1.3) then we get from Eq: 4.1.2: v bm = 1 m [P + P ohc v bm sξ bm ] (4.1.4) Writing Eq: Eq: and eq: together in vectorial notation yields: P ohc v bm ξ bm = H(P, P ohc, v bm, ξ bm ) (4.1.5) where H is a vectorial function. The initial conditions are x [0, l]: P ohc (x, 0) v bm (x, 0) ξ bm (x, 0) = 0 (4.1.6)
92 80 Initialization P ohc (x, t), v bm (x, t), ξ bm (x, t), and P (x, t) are known. compute: P ohc (x, t), v bm (x, t), and ξ bm (x, t) by Eq: compute P ohc (x, t + h t ), v bm (x, t + h t ), and ξ bm (x, t + h t ) by differential equation initial value method. compute G(x, t + h t ) by Eq: then, find P (x, t + h t ) by implementing the finite differences scheme on Eq: t = t + h t Figure 4.1: Time step is followed by spatial step. The algorithm is used to compute the simulation on the time domain.
93 81 Assume we know P ohc, v bm and ξ bm. The pressure difference,p, is an argument in function Thus, in order to compute P ohc, v bm and ξ bm derivatives, the pressure difference has to be known. The pressure difference P along the cochlear partition is computed by Eq:2.2.6, 2 P x 2ρβ(x) 2 A Substituting Eq: and Eq: yields: 2 ξ bm t 2 = 0 2 P x 2ρβ 2 ma [P + P ohc rv bm sξ bm ] = 0 (4.1.7) Define Q(x) as a function of the spatial variable x, and, Q = 2ρβ ma (4.1.8) G(x, t) = P ohc r(x, t)v bm s(x, t)ξ bm (4.1.9) Substituting Eq: and Eq: in Eq: yields, 2 P QP = QG (4.1.10) x2 These equations are subject to the boundary conditions Eq: , P x = 2ρS (t) x = 0 P (x, t) = 0 x = l where S(t) is the stapes velocity applied to the inner ear. Hence, solving Eq: gives the pressure and, therefore, Eq is solvable. The derivatives of P ohc, v bm
94 82 and ξ bm are known and, therefore, we can find the values of P ohc, v bm and ξ bm for the next time step. 4.2 Time Domain Computational Algorithm The solution in the time domain is performed in two sequential steps [57]. In the first step, the initial value condition problem is solved by an iterative method. In the second step, the boundary value problem is solved by the finite differences method. Figure 4.1 depicts the algorithm s flowchart. There are two steps, one step in time domain, and the other step in the spatial domain. The time domain model equations are solved numerically and therefore are solved on discrete two dimensional net. We assign h t to the time variable step size. The spatial variable x step size is h x = l/n and each point along the cochlear partition is denoted by x i. Assume the following variables for a particular time t = T : ξ bm, v bm, P ohc for every x i are known and the stapes velocity S (T ) is also known. Then, Eq: and it s boundary condition are well defined. An approximation to the pressure difference P can be obtained for every nodal point x i. We choose the finite difference method to solve the boundary condition problem. If the pressure differences between the scala: P, for every x i at this particular time t = T are known, then all the arguments in the differential equation Eq: and all the necessary initial conditions are known. An approximation to the following variables: ξ bm, v bm, P ohc at t = T + h t is achievable by an initial value numerical method. Thus, for time variable t = T + h t and for every x i we have an approximation to
95 83 the variables ξ bm, v bm, P ohc. The differential equation Eq: components and especially the magnitude of S(t), might undergo significant changes during the computation process. To keep t the computation error bounds subjecat to some criterion, the time step size should be bound. If the time step is too small the computation is not efficient and the error due to rounding increases. 4.3 Spatial Domain Solution The spatial step in the recurrent process is to find a solution to the second degree differential equation with boundary condition Eq: On the interval [0, l] we place a uniform net,say: x i = ih x h x = l N i = 0, 1,, N (4.3.1) A linear combinations of Taylor series at x = x i for P i 1 and P i+1,at each interior net point, x i i = 1, 2,, N 1 gives an approximation to the pressure P second derivative in x. Define u i as the approximated value of P xi, then, substitution of this approximation in Eq: gives: where Q i = Q(x i ) and G i = G(x i ). u i 1 (2 + h 2 xq i )u i + u i+1 = h 2 xq i G i (4.3.2) At the exterior points, Taylor series gives an approximation to the second derivative using the same method as in the frequency domain solution. Applying this approximation to the boundary conditions Eq: yields:
96 84 u 1 u 0 (1 + h2 x 2 Q 0 ) = 2h x ρs (T ) + h2 x 2 Q 0 G 0 u N = 0 (4.3.3) The boundary points equations Eq: and the interior node points equations Eq: are combined into a linear system: where we have introduced the N + 1 dimensional vectors: Au = F (4.3.4) u = u 0 u 1. u N 1 u N F = 2h x ρ S (T ) h 2 x 0.5G 0 Q 0 G 1 Q 1. G N 1 Q N 1 0 (4.3.5) and the N + 1 order matrix is written: ( h2 xq 0 ) 1 1 (2 + h 2 xq 1 ) 1 A = (4.3.6) 1 (2 + h 2 xq N 1 ) By the definition of Q Eq: 4.1.8, for i = 0, 1,, N 1, Q i > 0, hence matrix A has a dominant diagonal, Therefore, it is a regular matrix [80]. So there exists a unique solution to the linear system Eq: Moreover, matrix A can be factored in the bi-diagonal form since it is a tridiagonal matrix and for i = 0, 1,, N, Q i > 0. The proof is found in [24] page 55. Thus, the matrix A can be written as:
97 85 A = α 0 1 α α N 1 1 α N 1 γ 0 1 γ γ N 1 1 (4.3.7) where: α 0 = (1 + h 2 Q 0 x ) 2 α i = (2 + h 2 xq i ) γ i 1 i = 1, 2,, N 1 γ i = 1 α i i = 0, 1, 2,, N 1 (4.3.8) α N = 1 γ N 1 The terms Q i defined in Eq: do not change in time; therefore, the matrix A is time independent. The same matrix is used to solve Eq: for every time step. Thus, it has to be computed and factorized only once. The actual solution is implemented in two steps. In the first step we define an intermediate vector: g whose value is obtained by solving Eq: α 0 1 α α N 1 1 α N g 0 g 1. g N 1 g N = F 0 F 1. F N 1 The intermediate vector g is prescribed by the recursion formula: F N (4.3.9) g 0 = F 0 α 0 g i = F i g i 1 α i The second step requires solving Eq: i = 1, 2,, N (4.3.10)
98 86 1 γ 0 1 γ γ N 1 1 u 0 u 1. u N 1 u N = g 0 g 1. g N 1 g N (4.3.11) which yields the solution for Eq: 4.3.4: u N = g N (4.3.12) u i = g i γ i u i+1 i = N 1, N 2,, 1, 0 The operational count for the spatial domain solution procedure is somewhat striking. The spatial domain solution requires only 2N + 1 multiplication operations. 4.4 Time Step At the end of the spatial domain step, the pressure along the cochlear partition is known. We have approximations to the following variables: P, v bm, ξ bm and P ohc along the cochlear partition, at all time points that satisfy: t T. The purpose of the time step is to calculate v bm, ξ bm and P ohc at t = T + h t. The approximation is applied by numerically solving an ordinary differential equation Eq: In this research work,we have tried several numerical methods to approximate the above differential system solution. A one-step method - modified Euler method, a multi-step method, i.e. predictor corrector Adams Besforths - Adams Molton method, and an extrapolation method [80]. All the above methods gave similar results. We chose the modified Euler method, for its simplicity and computation efficiency.
99 Modified Euler Method The modified Euler method, which is also known as the trapezoidal method, is classified as Runge-Kutta method of order two. The trapezoidal method is known to be A-stable method which is an appropriate method for stiff differences problems [20]. To explain the trapezoidal method, we define an initial value problem: y = f(t, y) y(0) = Y (0) (4.4.1) Integrating the above differential equation over [t j, t j+1 ] yields y(t j+1 ) = y(t j ) + tj+1 t j f(ζ, y(ζ))dζ (4.4.2) where h t = t j+1 t j is the time step size. The integral is numerically approximated by the trapezoidal method [80], tj+1 t j f(ζ, y(ζ))dζ = h t 2 [f(t j, y(t j )) + f(t j+1, y(t j+1 ))] h3 t 12 y(3) (ζ j ) (4.4.3) where ζ j is a point in the time interval (t j, t j+1 ). Substituting Eq: in Eq: and ignoring the error term h3 t 12 y(3) (ζ j ) yields: y(t j+1 ) y(t j ) + h t 2 [f(t j, y(t j )) + f(t j+1, y(t j+1 ))] (4.4.4) The modified Euler method is a one-step method with an O(h 2 t ) order of convergence. Eq:4.4.4 is an implicit equation since y(t j+1 ) is on both sides of In order to solve Eq:4.4.4 we define an iterative series {w n }:
100 88 w 0 = y(t j ) + h t f(t j, y(t j )) w n+1 = y(t j ) + h t 2 [f(t j, y(t j )) + f(t j+1, w n )] (4.4.5) The first element in the series defined in Eq: is obtained by Euler method. If the iterative series {w n } is convergent, then its limit is equal to the solution of Eq: The series defined in Eq: is repeated until convergence is obtained. If we assume that the function f obeys the Lipschitz condition in the second variable, the series converges. In order to prove it, subtraction of Eq: from gives: y(t j+1 ) w n+1 = h t 2 [f(t j+1, y(t j+1 )) f(t j+1, w n )] (4.4.6) Assuming that the function f obeys the Lipschitz condition in the second argument with a constant L yields, Therefore, if y(t j+1 ) w n+1 Lh t 2 y(t j+1) w n (4.4.7) Lh t 2 < 1 then the iterative series {w n } converges to y(t j+1 ). In particular: y(t i+1 ) w n < Lh t 2 n y(t i+1 ) w 0 (4.4.8) Hence, if the function f, obeys the Lipschitz condition and h t is small enough, then the iterative process suggested by Eq: converges. Furthermore, if y(t j+1 ) w 0 is known, the number of iterations needed to gain a desired accuracy can be evaluated.
101 89 It is rather complicated to evaluate the Lipschitz constant L for the functions we deal with, Eq: 4.1.1, Eq: 4.1.4, and Eq: Therefore, the convergent estimation by Eq: is not applicable. Often, in practice, the step size h t and the initial guess are chosen to ensure that only one or two iterations are needed. The truncation error of the modified Euler method is O(h 3 t ) ( Eq: 4.4.3), therefore there is no benefit to compute the iterative series {w n } more accurate then O(h 3 t ). To maintain this order of accuracy, the eventual iteration w n, which is chosen to represent y(t i+1 ), should satisfied y(t i+1 ) w n+1 = O(h 3 t ). On the other hand, applying the explicit first iteration step, the Euler step gives: y(t j+1 ) w 0 = O(h 2 t ) (4.4.9) Therefore, substituting Eq: in Eq: implies that only one iteration is needed to maintain the same order of truncation error. Thus, if h t is rather small, then the first iteration step truncation error is of order O(h 3 t ). w 1 = y(t j ) + h t 2 [f(t j, y(t j )) + f(t j+1, y(t j ) + h t f(t j, y(t j )))] (4.4.10) Eq: is called the difference equation associated with the modified Euler method. The local truncation error measures the amount by which the difference equation approximation fails to satisfy the exact solution of the differential equation. The difference method has a local truncation error given by: τ j+1 (h t ) = y(t j+1) w 1 h t (4.4.11)
102 90 Substituting Eq: in Eq: yields: τ j+1 (h t ) = y j+1 y j f(t j, y j ) + f(t j+1, y j + h t f(t j, y j )) h t 2 (4.4.12) If the function f is second order differentiable, then by a second order Taylor polynomial in two variables it can be shown [80] that: τ i+1 (h t ) = O(h 2 t ) The simple Euler method in which the truncation error is of order τ i (h t ) = O(h t ) [80]. Hence, by one more iteration, we gain a method with the local truncation error of O(h 2 t ). The assumption we made, i.e., that the function f is a second order differentiable function (SODF), is reasonable for the following reasons: It is reasonable to assume that the cochlear partition velocity ξ bm /dt is SODF. The sigmoid function f nl in is SODF, which means that P ohc is also SODF. The fact that P ohc is SODF together with the fact that r(x, t) [ Eq: ], s(x, t) [ Eq: ] are SODF, means that G(x, t) [Eq: ] is SODF. Therefore P(x,t) [Eq: ] is SODF. Hence, all the terms in Eq: are SODF. Thus, if cochlear partition velocity is SODF then the assumption about the SODF of f is correct. Consistency The one-step difference equation method with local truncation error τ(h t ) at the jth step is consistent with the differential equation it approximates if: lim max τ j = 0 h t 0 1 j N Thus, both the simple and modified Euler s methods are consistent [20].
103 91 Convergency The one-step difference equation method converges with respect to the differential equation it approximates if: lim max ỹ j y(t(j)) = 0 h t 0 1 j N where y(t j ) denotes the exact solution of the differential equation and ỹ j is the approximation obtained from the difference method at the jth time step. It is clear that both methods converge [20] Error Control and Variable Step Size Method The modified Euler method local truncation error is of order O(h 2 t ) [80]. To ensure that the modified Euler iterations converges, we have to be sure that the time step size is adequate. We cannot implement Eq: but we can estimate the truncation error by using the simple Euler step, which is included in the modified Euler routine. The modified Euler method computation is composed of two steps. The first step is a prediction of the differential equation solution by a simple Euler method. The simple Euler method local truncation error is of order O(h t ) [80]. The second step is another approximation of solution of the differential equation. Thus at completion of the second step, where the modified Euler finial outcome is computed, we have two approximations with local truncation error of order O(h 2 t ) and O(h t ). These two outcomes are the key to the truncated error estimation. Let us assume that the initial value y j = y(t j ) is exact. Assign w 0,j+1 and w 1,j+1 to the outcomes of Euler and modified Euler methods and τ j+1 (h t ) and τ j+1 (h t ) to
104 92 their local truncation errors. Thus, by truncation error definition we obtain: which yields, τ j+1 (h t ) = y j+1 w 0,j+1 h t (4.4.13) τ j+1 (h t ) = y j+1 w 1,j+1 h t (4.4.14) τ j+1 (h t ) = τ j+1 (h t ) + w 1,j+1 w 0,j+1 h t (4.4.15) Since τ j+1 (h t ) is of order O(h t ) and τ j+1 (h t ) is of order O(h 2 t ), the significant portion of τ j+1 (h t ) must come from the right hand term of equality This gives us an easily computed approximation for the Euler method local truncation error. τ j+1 (h t ) = w 1,j+1 w 0,j+1 h t (4.4.16) However, the object is not simply to estimate the local truncation error but to adjust the step size to keep it within a specified bound. Since that τ j+1 (h t ) is of order O(h t ) a number K independent of h t exists. τ i+1 (h t ) Kh t (4.4.17) Suppose that we apply another step size qh t, then its truncation error is given by: τ j+1 (qh t ) = O(qh t ) Kqh t (4.4.18) Substituting Eq: and Eq: in Eq: yields, τ j+1 (qh t ) q τ j+1 (h t ) = q w 1,j+1 w 0,j+1 h t (4.4.19)
105 93 Suppose that the truncation error is bounded by ɛ, then: From Eq: we get: ɛ τ j+1 (qh t ) ɛ q w 1,j+1 w 0,j+1 h t (4.4.20) q ɛh t w 1,j+1 w 0,j+1 (4.4.21) If the ratio q from Eq: is less than 1, then the time scale step size is decreased by a multiple of less than q. On the other hand, if the ratio q is greater than 1, then the step size increase procedure is more sophisticated [80] Convergence and Stability We chose the trapezoidal or modified Euler method because it is a consistent and convergent method [1]. Moreover, the method is A-stable which means that it is good candidate to solve stiff differential equations [1]. A numerical method is A-stable if the numerical solution for the differential equation: y = λy, where Real(λ) < 0, asymptotically approaches zero as the steps number n [20]. The differential equations involved have many and different scaled time constants, therefore it is important to choose a method that is A-stable, such as the modified Euler method. An equivalent definition for A-stable is that the method s region R of absolute stability contains the entire left half-plain. It can be show quite easily that the modified Euler method is A-stable [1]. Consider the modified Euler method applied to the linear equation: y = λy + g(x) (4.4.22)
106 94 y(0) = Y 0 (4.4.23) namely y n+1 = y n + h 2 (λy n + g(x n ) + λy n+1 + g(x n+1 )) (4.4.24) for n > 0 and y 0 = Y (0). To analyze the stability of the method, let us define the perturbed series: z n+1 = z n + h 2 (λz n + g(x n ) + λz n+1 + g(x n+1 )) (4.4.25) for n > 0 and z 0 = Y (0) + ε. Let us define the difference series as: w n = z n y n. Subtracting Eq: from Eq: gives: for n > 0 and w 0 = ε. w n+1 = w n + λh 2 (w n + w n+1 ) (4.4.26) This reads as: which implies by induction: 1 + λh 2 w n+1 = w n 1 λh 2 (4.4.27) In the case that Real(λ) < 0, Eq: yields, w n+1 = ε( 1 + λh t 2 ) n (4.4.28) 1 λht 2 lim w n = 0 (4.4.29) n In other words, the modified Euler method does not require any restriction on the step size in order to ensure stability. We hasten to say that this does not mean, of
107 95 course, that any h t is suitable. It is necessary to choose h t > 0 small enough to ensure that the local truncation error is within reasonable bounds and the exact solution is adequately approximated Time Solution Algorithm Summary The model is composed of one boundary value equation and three initial value equations. The simulation algorithm is depicted in Figure 4.2. The algorithm uses a fixed resolution along the cochlea, but variable time steps. The decision whether and how to change the step size is carried out by comparing the differences between the result of the modified Euler method and the result of a first order Euler method. The algorithm changes over to the next time step if the estimated truncation error, for all nodal points, is less than some threshold. At every time step, the values are first computed by an Euler method, and then the same values are computed by the modified Euler method. The difference between the results of the two methods is the convergence criterion of the algorithm.
108 96 Initialization compute ξ bm, ξ bm and P ohc by compute ξ bm, ξ bm and P ohc by the the Euler method modified Euler method compute P by the compute P by the finite differences method finite differences method compute current values of ξ bm and P ohc compute current values of ξ bm and P ohc compare the values of ξ bm, ξ bm and and P ohc to the values received in the previous iteration, and to the values received from Euler method. Are the iterations outcome close enough? Are the step size suitable? close enough. very close. not close at all. not close enough. Go to the next step Increase step size by 2 multiple Decrease step size. Restart time step Do another iteration Figure 4.2: Flow chart of the time domain simulation
109 Chapter 5 Time Domain Simulation Computation Analysis The algorithm was implemented as a C++ program. The program was tested with several input signals, different amplification functions γ(x), etc. The model output was a two dimensional matrix of basilar membrane velocities, that was sampled at 50 khz. The matrix dimension was time and spatial. This program was used to test the computation analysis aspects. In this chapter, we describe the errors obtained while using different parameters, and the program running time dependencies due to spatial step size h x, and time step size h t. 5.1 Computation Accuracy Since there is no analytical solution to the model equations, a reference set of parameters was defined in order to evaluate the significance of the different step sizes of the model. The number of nodal points was prescribed to 4097 nodes, i.e, h x = l/4096 = 3.5/4096 cm, and the maximum step size in time was max(h t ) = 1µ Sec. The model was tested for different sets of step size and for different input signals. 97
110 98 The results, velocities matrices given for different values of step size, were compared to the the results of the reference set. We used simple mean square error with weight function= 1 to estimate the difference between the matrices. The number of nodal points along the spatial domain was chosen in the range [257, 513, 1025, 2049, 4097]. The reason for the choise of the values 2 n + 1, was to enable decimation in the spatial dimension Time Step Figure 5.1 depicts the mean square error (MSE) result as a function of the maximum allowed time step size. We measured the accuracy of the model output by comparing the results of the model, to the same results generated in the highest resolution (i.e. maximum step size of 1e 7 sec, and 4097 sections along the cochlea). We computed the mean square error between the two matrices. The model was tested with equal weight sine waves at frequencies: 250 Hz, 500 Hz, 750 Hz, 1 khz, 2 khz,4 khz,8 khz. The duration of the test signal was 100 msec. It can be seen that below 1µSec step size, accuracy hardly improved when h t 1µSec the dominant error source is the spatial resolution. Similar results were obtained for other inputs like speech. click, and chirp Spatial Step Figure 5.2 depicts the resultant matrix MSE versus the cochlear resolution, i.e., the number of equal spaced spacial net points. The model was tested with voice signal sampled at 50 khz. Each line describes different maximal time step size. As one could expect, the higher the cochlear resolution is, the better the accuracy. Looking at the line corresponding to max(h t ) = 1µs reveals that 513 or 1025 net points are
111 99 Figure 5.1: Result accuracy. The mean square error, as a function of the maximum time step size for the sin wave. Different lines are drawn for different cochlear resolutions.
112 Figure 5.2: Spatial resolution vs MSE. The test signal was the word mi. Different lines are drawn for different maximum time step size. 100
113 101 good choices. 5.2 Time Versus Frequency Simulation Figure 5.3 depicts a comparison between the simulations in the time and frequency domains for the same model parameters. Although the responses of the simulations resemble each other, they are actually quite different. The time domain simulation is less accurate than the frequency domain. There are several reasons for the decreased accuracy of the time domain. The time domain response,depicted in Figure 5.3 is the log of thesquared velocity s average. Therefore, equal conditions between those simulation means running the time model for very long periods, etc. But longer simulation periods means greater error because we numerically solve differential equations. Thus, if the simulation time is too small, we have errors due to the zero velocity and zero displacement initial conditions; and when the simulation time is long we have errors due to the numerical process. The time domain solution approximates the real solution in every time or spacial step. This approximation causes truncation errors. There is an enormous difference between the number of computations between the time and the frequency domain methods, thus the accumulated rounding error in the time domain simulation is much higher than in the frequency domain. Thus, the accumulated result is that the time domain simulation is less accurate than the frequency domain. But, at the same time, the simulation in time domain is an essential tool for nonlinearities signals and for non-stationary inputs. The frequency domain simulation is superior to the time domain for single tone with low amplitude simulation where the responses are linear. The reason for this is that the numeric error is much smaller and the computation is significantly more
114 102 Figure 5.3: The time domain and the frequency domain simulation for 1 khz tone with the same set of parameters. Continues line for time domain and dashed line for frequency domain. efficient. The major shortcoming of the frequency domain simulation is that it is not usable for a wide range of stimulus levels because it s linearity assumption is substantial. The time domain simulation is used to obtain model responses for complex stimuli such as chirp, signals composed of tones with different frequencies and different level ranges, speech, and noisy signals.
115 Chapter 6 Simulation Results 6.1 Introduction The model simulations for both normal and impaired ears are presented in this chapter. The most pronounced phenomena related to hearing loss are audiogram shift and boarder tuning curves. The model simulations exhibit clear differences between normal and impaired ears. The intelligibility of speech is another indication of normal hearing. The model responses to speech and to speech with noise might emphasize the difficulties of the neural system in the brain to recognize phonemes. The difficulties are more evident for impaired hearing responses. The parameters used for the simulations are presented in table The Model Responses to a Sine Wave In order to demonstrate how the model predicts the difference between normal ears and ears with OHC loss, we chose to present the basilar membrane velocity (BMV) along the cochlea partition as a response to sine waves at low levels. It is quite accepted that inner ear responses are linear for low level stimuli magnitudes. Hearing threshold measurement ( not under masking ) is usually done in magnitude ranges in 103
116 104 List of model Parameters Parameter Value/Definition units Description l 3.5 cm Cochlear Length ρ 1 gr/cm 3 Density of perilymph β cm Width of the basilar membrane A 0.5 cm 2 Cross-sectional area of the cochlea scalae m e 1.5x gr/cm 2 Basilar membrane mass per unit area s e 1.5x gr/cm 2 sec 2 Basilar membrane stiffness per unit area r 0.25e 0.06x gr/cm 2 sec Basilar membrane resistance per unit area ω OHC 1kHz rad/sec Outer Hair Cell membrane cutoff frequency which the cochlea is regarded linear. Table 6.1: List of model Parameters The BMV curves were obtained by computing the velocity s Fourier coefficient absolute value. Let assume that the BMV is in good correlation with neuronal rate responses, hence the BMV simulates the neuronal rate or the excitation patterns. Figure 6.1 represents calculation of the average BMVs for various sinusoidal inputs. Each set of the average BMVs was obtained with a different value of γ. In these simulations, a fix γ was considered along the whole cochlear partition. It is obvious from Figure 6.1 that with increase of γ the location of the resonance for each input frequency moves towards the helicotrema, and the peak at the resonance becomes more significant, especially for frequencies above 1kHz. 6.3 Comparison between models result and measured data Our model parameters were based on human cochlea because we aimed to explain hearing impairment in humans. In an effort to make a comparison to measurement, the result of our model was compared to measurements that were done on Chinchillas. The Approximate hearing frequency range of Chinchillas is 90 22, 800Hz [82] which
117 Figure 6.1: Partition velocity patterns (BMV) as function of different γ and for different input frequencies. 105
118 Figure 6.2: comparison between Ruggero et al [59] measurements and our model. Ruggero s measurement were normalized versus the stapes velocity and versus the human frequency range. Ruggero s results depicts as red segments which describe the basilar membrane velocity in a 12dB range. The continuous lines depicts our model isointensity curves as a function of the parameter γ. 106
119 107 is quite similar to human s. The measurements that we tried to compare, were published by Ruggero et al [59]. In Figure 6.2 we show comparison between Ruggero s results and our model. The low edge of the red segment depicts measurement of basilar membrane velocities for low level stimuli: [db] SP L, versus the frequency of the stimulus.. The adaptation of the Chinchilla s result to human cochlea was done by the following procedure: The Chinchilla s measurement were taken at 3.5[mm] from the oval window. The corresponding site of measure in human is at 8.75[mm] from the oval window. This computation follows that we assume that the Chinchilla cochlea length is 14[mm] ( Chinchilla cochlea length is [mm] according to Bohne [8] or 13 14[mm]according to Stefan et al [53]). This site on the human basilar membrane matches characteristic frequency(cf) of 4KHz. On the other hand, the Chinchilla CF at the measurement site was 10KHz. Therefore, the frequency variable was transformed by the formula: f human = 4 10 f Chinchilla. Ruggero s measurement gain axis was transformed into nonunit scale by the following procedure: Ruggero s graphes depicts the gain in mm secp a units. The measurements also contain the stapes velocity for each frequency. Using the stapes velocity, a normalization procedure is done. The normalization is done by dividing basilar membrane velocity by stapes velocity. In his paper, Ruggero wrote that the Chinchilla surgery induced CAP threshold shift at CF of at least 6 12dB. The red horizontal segment in Figure 6.2 depicts this range. The continuous lines depicts the basilar membrane velocity versus frequency for isointensity stimuli and due to the stapes velocity normalization, the gain axis has no units, mm/sec. This measurement to model results similarities is not unique to this mm/sec Chinchilla to human calibration and can be obtained for other Chinchilla to human
120 108 frequency mapping. To make this comparison more visible, the isointensity curves of Ruggero et al are shown in Figure 6.3. The comparison shown in Figure 6.2 supports choosing the OHC gain variable γ = 0.5 as a characteristic of normal hearing. Figure 6.3, from Ruggero et al [59] depicts the cochlea gain, which was calculated as the basilar membrane velocity mm/sec versus the sound level P a within 2mm of the tympanic membrane. The stapes gain is also known and it is depicted as a thick line at the bottom of the figure. Therefore the ratio between the stapes velocity and the basilar membrane is known. Our model results the ratio between the oval window velocity or the stapes velocity and the basilar membrane velocity. This can be easily seen by the boundary condition in Eq Therefore, our model predicts and Ruggeros measurement in 6.2 are related to the same physical quantities. Linearity is one of the assumptions in the frequency domain model. This assumption was justified due to restriction of the stimulus to low level. Therefore, the calculated gain represents the frequency model fully and there is no need for absolute units. Sharpening of the BMVs can be obtained by decreasing the partition damping factor. It is questionable whether the OHC-embedded model sharpening contribution to tone stimuli responses could be achieved by the one-dimensional model with a low partition damping factor. It is well known that a low damping factor results in a sharp peak in the basilar membrane velocity curves. The sharpening caused by the low damping factor is not realistic due to the tip and tail gain [43]. This is the primary reason that those models were abandoned. Figure: 6.4 depicts the contribution to sharpening due to a decrease in the damping factor and OHC gain increase. The model was tested with an 8 khz sine wave and a different set of parameters. The solid line depicts the response obtained by low damping factor while the dash-dot line
121 Figure 6.3: Isointensity curves from Ruggero et al [59]. A family of isointensity curves representing the gain (velocity divided by stimulus pressure) of basilar membrane responses to tone beeps as a function of frequency (abscissa) and intensity ( parameter in db SPL ). The thick line at the bottom indicates the average motion of the stapes. 109
122 110 Equal responses peak parameters. γ r 0 Figures Line legend 0 0.4e 2 dashed line e 2 solid line e 2 dashed-dot Table 6.2: OHC gain γ and damping factor r 0 parameters, which result BMVs curves with equal peak height. corresponds to high OHC gain. Three responses are presented: the average BMVs peak was equal for two of them. The parameter combinations of these responses are listed in table 6.2. As can be seen in Figure: 6.4, the embedded OHC model sharpening results are more realistic than the one-dimensional model with decreased damping factor. 6.4 Tuning Curves Tuning curves are the most common representation of cochlear partition motion. Tuning curves are obtained by stimulating the ear with tones. A tone has two parameters, frequency and magnitude. Tuning curves are sets of all combinations of magnitude and frequency that yield constant response at certain locations along the cochlear partition. The responses can be either constant rate of spikes measured from certain neuronal fiber, or basilar membrane velocity at certain places along the basilar membrane. The tuning curves were computed by interpolation. The interpolation points were obtain by the BMVs. For specific sets of cochlea parameters, a BMV is a function from R 2 to R n, where the domain parameters are the input signal frequency and magnitude. The function range is a vector of absolute value of the velocity at n mesh points along the cochlea partition. For certain locations along the cochlear partition and for certain input signal frequency, the attenuation between the input signal and
123 Figure 6.4: Comparison between the decreasing of damping factor and OHC gain factor increase. The y axis is the relative basilar membrane velocity [db]. For Low damping factor with zero OHC gain - solid line, high damping factor with High OHC gain - dash-dot line, zero OHC gain with high damping factor - dashed line. The exact values are given in table
124 112 the membrane velocity is easily computed. Hence, if the partition velocity absolute value is held constant for specific locations along the cochlea partition, then a match between the input signal frequency and the attenuation is found. Since the model is linear, the amount of input signal amplification is equal to the computed attenuation. In nonlinear models, the BMVs are obtained from the time domain simulation. The procedure of computing the attenuation is not valid in the nonlinear case since the response is a nonlinear function of the input signal magnitude. The computation is done by initially computing a set of BMVs with the same input frequency and with increasing input magnitudes. Then, the input magnitudes segment which contains the adequate value is chosen. A simple linear interpolation will provide an approximation to the corresponding value. Figure 6.5 represents tuning curves obtained for different places along cochlea partition, which correspond to different characteristic frequencies, and for two OHC gain values, γ = 0 and γ = 0.9. As the value of γ approaches 0.9 ( γ [0, 1)) the dip of the curve is sharper. The parameter range γ as shown in Figure 6.5 is not realistic. These graphs are included only to show the dynamic range of the γ parameter. In principle, these results resemble the scheme of normal and damaged hearing due to OHC dysfunction [14]. 6.5 Comparison between models tuning curves and measurements The same procedure we made for comparison between models isointensity curves and measurement was applied for tuning curves. The measurements were taken from the same paper, written by Ruggero et al [59]. The same frequency adaptation from the
125 113 Figure 6.5: Tuning curves obtained by the time domain solution. Simulated tuning curves derived by two values of γ. continuous lines represents γ = 0. For totally dysfunction OHCs, the doted lines represents γ = 0.9
126 114 Chinchilla frequency range to human frequency range was done. Figure 6.6 depicts model s tuning curves versus measurement. The continuous lines assigned for model s tuning curve with different values of γ and the red lines, with + sign, and the blue lines, with sign, represent average frequency - threshold tuning curves from the auditory nerve fibers with CFs of 8-12 KHz and isovelocity curve 25 µm. The comparison described in Figure 6.6 supports the decision Sec made later on to choose γ = 0.5 as a representative OHC gain for normal hearing. For the sake of clearness, the Graph from [59] is shown in Figure Audiogram Simulations Loudness corresponds to the subjective impression of the magnitude of a sound. The formal definition of loudness is: that attribute of auditory sensation in terms of which sounds can be ordered on a scale extending from quiet to loud. For the purpose of estimating the model outcomes in terms of this perceptual concept, we will use the following definition: Loudness in terms of the model L d, is the energy acquired by the whole cochlea due to the basilar membrane velocity [56] L d = 1 T T l 0 0 ( ξ bm (x, t)) 2 dxdt (6.6.1) where T is the stimulus duration and l is the cochlea length. Human cochlear activity is best described by its audiogram, which is the threshold obtained for different stimulus frequencies relative to an ideal cochlea. Thus, we can use the model simulation for computing loudness in order to estimate the measure of hearing loss, which is a sort of audiogram estimation. Since γ was defined in the interval [0, 1], where γ = 0 represents a cochlea with
127 Figure 6.6: The Figure depicts comparison between model s tuning curves obtained by the frequency domain solution and data from [59]. Continuous lines assigned for the model s tuning curve with different values of γ. The red line with + marks is an average frequency - threshold tuning curve computed from the rate thresholds of Chinchilla auditory nerve fibers with CFs of 8-12 KHz and high spontaneous activity. The blue line with presented a measured isovelocity curve 25 µm Sec. 115
128 116 Figure 6.7: From ruggero [59]. Thin solid lines represent isovelocity contours for responses of 25, 50, 100, 200, 400 µm and dashed line assigned for isodisplacement contours [nm]. The thick solid line is an average frequency - threshold tuning Sec curves computed from the rate thresholds of Chinchilla auditory nerve fibers with CFs of 8-12 KHz and high spontaneous activity.
129 117 totally dysfunctional OHC, and γ = 1 represents a nonrealistic cochlea whose motion approaches infinity, we chose γ = 0.5 to represent normal hearing. This choice of γ, fits the comparison between models result and measured data in Figure 6.2. The baseline of the audiogram is the threshold obtained for an ideal cochlea. Figure 6.8 depicts the hearing threshold curves obtained for different values of γ. The estimation of the threshold curves was obtained by two steps. First, the stapes velocity resulting in constant loudness was calculated. Second, the pressure level which produces this stapes velocity was obtained by the sound pressure to stapes footplate velocity transfer function SVTF. The SVTF characterizes the stapes velocity to the ear canal pressure ratio. The data of the SVTF was obtained from human cadavers, cochleae [73]. The low stimulus level result linearity of the model, linearity of the loudness, definition 6.6.1, and linearity of the SVTF therefore support that the whole transformation is linear. Hence, the inverse transformation is easy to obtain. The dashdot in Figure 6.8 depicts the stapes velocity versus the ear canal pressure (SVTF). The SVTF units are mmsec 1 P a 1. The SVTF present in Figure 6.8 is given in db scale. A comparison to minimum audible pressure (MAP) [9], may suggest that γ = 0.5, presents a reasonable choice. We can use the SVFT to estimate the velocity of the cochlear partition in response to the ear canal pressure. Let us assume that the SVFT gain is -30 db, Figure 6.8. For γ = 0.5, the cochlear partition to stapes velocity ratio is 30 db at the peak, Figure 6.2. Therefore, the cochlear partition peak velocity to pressure level ratio is 0 db. Now assume that the stimuli level is 10 dbspl, that is 200 µp a, thus we get 200 µmsec 1. These values of pressure and velocity are in the same scale as roggeros
130 Figure 6.8: Threshold estimation curves. Each of the continuous lines depict a threshold versus stimulus frequency curve for γ {0.8,..., 0.1, 0}. The dashdot line depicts the outer and middle ear transfer function: SVTF. The SVTF is given in db scale and depicts the the stapes velocity to the pressure level near the tympanic membrane ratio. 118
131 119 results [59]. Let us define θ(ω, γ) as the estimated measure of hearing loss obtained by the model for an input signal frequency ω and a cochlea with an outer hair cell gain γ. θ(ω, γ) = L d (ω, 0.5) L d (ω, γ) (6.6.2) Thus θ(ω, 0.5) = 0, for all ω. Figure 6.9 depicts the estimated measure of hearing loss for different values of γ. The estimated measures of hearing loss obtained for cochleae with γ > 0.5 reveal thresholds that are better than that of the ideal cochlea. The difference in the estimated thresholds for different values of γ is less than 20 db for input frequencies below 1 khz. However, there is a significant difference in the estimated threshold for higher frequencies. For γ < 0.2, each of the estimated measures of hearing loss has a maximum threshold at a frequency between 4 and 6 khz. These types of measure of hearing loss resemble typical phonal trauma audiograms. Higher values of γ (γ > 0.5), however, result in estimated measure of hearing loss with decreased threshold as a function of frequency. Those types of estimated measure of hearing loss are not realistic, since they are not found among human audiograms. As was defined earlier, a normal healthy cochlea is one whose outer hair cell gain γ is equal to 0.5 and a cochlea with outer hair cell loss is presented by γ < Variable γ Most studies that measured outer hair cells loss on human or animals(liberman and Dodds; Saunders et al [62, 45]) demonstrated that the outer hair cell loss typically starts at the basal part of the cochlear partition and gradually expands toward the helicotrema.
132 Figure 6.9: Plots of hearing loss with respect to audiograms. Simulated hearing loss, derived by various values of γ. 120
133 Figure 6.10: (b) Estimated hearing loss for decreasing γ. Different types of outer hair cell hearing loss as characterized by the outer hair cell gain in (a). 121
134 122 In order to test the model prediction for such a case, we assumed a gradual change in γ(x), and calculated the corresponding measure of hearing loss. Figure 6.10(a) presents a set of outer hair cell gains obtained by γ(x) = 0.5(1 exp αx ), for different values of α. The corresponding estimated measures of hearing loss curves are presented in Figure 6.10(b). The plots of the estimated measures of hearing loss resemble hearing-impaired human audiograms typically found among the elderly. There is almost no hearing loss at low frequencies below 1 khz, but there is a gradual decrease in hearing for higher frequencies. The threshold shift extended 50 db at the frequency region correspond to the damaged area, Figure 6.10 (b). The same type of hearing loss result of kanamycin sulfate injection into Chinchilla s cochlea was reported by Ryan, Dallos and McGee [75]. They measured the hearing threshold shift in Chinchillas due to kanamycin injection. An estimation of the remains OHC percentage along the cochlea partition was done postmortem. Figures 1 and 2 in [75], present the correlation between the percentage of remaining OHC and the hearing threshold shift. These figures resemble the shape and the measure of our model estimation in Figure The outer hair cell gain γ(x), can also be interpreted as the density of the functioning outer hair cell along the cochlear partition. It is reasonable to assume that this density is not fixed along the cochlea, but varies randomly along the cochlea. We assume that γ(x) is a Gaussian random variable with a mean of 0.5 and standard deviation σ. The BMV obtained for different values of σ is shown in Figure 6.11 and the corresponding curves of estimated hearing threshold are shown in Figure 6.12.
135 Figure 6.11: Simulation of the Partition velocity responses for different stimulus frequencies and normally distributed γ with a mean of 0.5 and different values of variance σ. Each BMV was obtained from 50 simulations. 123
136 Figure 6.12: Plots of hearing loss obtained for normally distributed with a mean of 0.5 and different values of variance σ 124
137 125 The baseline threshold in Figure 6.12 corresponds to γ(x) = 0.5, which corresponds well to the comparison to measurements depicts in Figure 6.2 and Figure 6.6. Each BMV shown in Figure 6.11 was obtained from 50 runs of the model, where a different γ(x) was generated for each run. It is clear from Figure 6.11 that low values of σ yield similar BMVs to those obtained by a fixed γ as shown in Figure 6.1. However, for larger values of σ, the BMVs lose their significant peaks and they resemble the BMVs in Figure 6.1 that were obtained for γ = 0. Figure 6.12 depicts the audiograms which were obtained for OHC gain with constant mean E(γ) = 0.5, and several standard deviations σ. An evident maximum threshold was obtained at 4 khz when σ > A maximum threshold of 60 db was obtained for σ = 0.1. The resultant audiograms resemble typical noise-induced hearing loss audiograms. 6.8 Representation of the Dynamic Properties of Acoustic Signals The simulation in the frequency domain is restricted to a single tone with infinite duration. For signals composed of several tones with different frequencies, we can use the superposition principle. But for more complicated signals like speech or music, simulation in the frequency domain is impossible. In order to demonstrate the dynamic properties of the model, we tested the model response to a chirp. The chirp signal is defined as : sin(αt 2 )and its response is plotted in Figure The time domain simulation response, or the time place representation, is a two-dimensional matrix. The matrix rows represent the longitudinal axis of the cochlear partition and
138 126 the matrix column represents the time axis. The time axis resolution is prescribed by constant sample rate of 50 KHz. The longitudinal resolution depends on the number of equal length section used for simulation. We used 512 sections. The elements of the matrix represent the absolute value of the cochlear partition velocity in decibels units. This representation is conceptually similar to a spectrogram representation of a signal. The time domain matrix response is different than the spectrogram in the different frequency scales and in the time continuity feature compared to the windowing FFT and overlap and add used by the spectrogram. The upper Figure of Figure 6.13 depicts healthy cochlea simulation i.e. γ = 0.5, while the lower Figure is for dysfunctional OHC, i.e. γ = 0. It is clear, c.f page: Figure 6.13, that the frequency selectivity is better for γ = 0.5, than for γ = 0. The result shown in Figure 6.13 was expected since Figure 6.1 emphasizes the same observation that γ increase results sharper excitation patterns. Figure 6.13 reveals the importance of the time domain simulation. The time domain and frequency domain simulations give similar result for tones while the time solution can predict model results for complex signals. This simple chirp simulations shows different morphology of the time frequency response, caused by different γ. Amplification of the input signal result constant offset, therefor the picture morphology will not change. Speech intelligibility is concerned primarily with the ability to identify phoneme, words, etc. The first stage in the identification process is performed in the cochlea. Therefore it is of interest to see the differences between normal and impaired cochlea responses to speech signals. Figure 6.14 depicts a spectrogram of the signal shen, a Hebrew word composed of two phonemes. In Figure 6.15 the time - place representations of a normal and an impaired ear is
139 127 Figure 6.13: Response to chirp by normal and impair ear. The upper Figure depicts a functioning OHCs, i.e. γ = 0.5, while the lower Figure depicts a dysfunction OHCs γ = 0.
140 Figure 6.14: Spectrogram of the word Shen in Hebrew. 128
141 129 plotted. The upper Figure shows normal cochlear model responses i.e. γ = 0.5, while the lower Figure represents cochlear model responses with dysfunctional OHC; that is γ = 0. It is noticeable from Figure 6.15, that the result of a normal ear are much similar to the spectrogram depicted in Figure If we assume that there are common aspects between identification in the visual system and in the auditory system, then Figure 6.15 might suggest that the OHC model can explain the well-known identification differences between normal and impaired ears. 6.9 Signal in Noise It is of interest to test speech intelligibility under conditions of noise. It is known that one of the most difficult tasks for people suffering from impaired hearing is to identify speech embedded in a noisy ambiance. Figure 6.16 depicts model responses for the word shen in a noisy ambiance. The upper Figure represents normal ear, γ = 0.5, while the lower one represents an impaired ear, γ = 0. Comparing the upper and lower Figures in Figure 6.16 to Figure 6.15 reveals that the model response to a normal ear is more similar to the word shen depicted in Figure 6.15, but it can hardly imply that the OHC improved the intelligibility. We suppose that to gain noise reduction, one need to incorporate nonlinearities in the OHC s model.
142 130 Figure 6.15: Model response to the word shen. Upper Figure depicts cochlear model with γ = 0.5, while the lower Figure depicts a model with γ = 0
143 131 Figure 6.16: Simulation results for the word Shen in a noisy ambiance. Upper Figure depicts cochlear model with γ = 0.5 while the lower Figure is for disfunction OHC i.e. γ = 0
SOLUTIONS Homework #3. Introduction to Engineering in Medicine and Biology ECEN 1001 Due Tues. 9/30/03
 SOLUTIONS Homework #3 Introduction to Engineering in Medicine and Biology ECEN 1001 Due Tues. 9/30/03 Problem 1: a) Where in the cochlea would you say the process of "fourier decomposition" of the incoming
SOLUTIONS Homework #3 Introduction to Engineering in Medicine and Biology ECEN 1001 Due Tues. 9/30/03 Problem 1: a) Where in the cochlea would you say the process of "fourier decomposition" of the incoming
Auditory System Feedback
 Feedback Auditory System Feedback Using all or a portion of the information from the output of a system to regulate or control the processes or inputs in order to modify the output. Central control of
Feedback Auditory System Feedback Using all or a portion of the information from the output of a system to regulate or control the processes or inputs in order to modify the output. Central control of
Structure, Energy Transmission and Function. Gross Anatomy. Structure, Function & Process. External Auditory Meatus or Canal (EAM, EAC) Outer Ear
 Gross Anatomy Structure, Energy Transmission and Function IE N O ME 1 Structure, Function & Process 4 External Auditory Meatus or Canal (EAM, EAC) Outer third is cartilaginous Inner 2/3 is osseous Junction
Gross Anatomy Structure, Energy Transmission and Function IE N O ME 1 Structure, Function & Process 4 External Auditory Meatus or Canal (EAM, EAC) Outer third is cartilaginous Inner 2/3 is osseous Junction
Mechanical Properties of the Cochlea. Reading: Yost Ch. 7
 Mechanical Properties of the Cochlea CF Reading: Yost Ch. 7 The Cochlea Inner ear contains auditory and vestibular sensory organs. Cochlea is a coiled tri-partite tube about 35 mm long. Basilar membrane,
Mechanical Properties of the Cochlea CF Reading: Yost Ch. 7 The Cochlea Inner ear contains auditory and vestibular sensory organs. Cochlea is a coiled tri-partite tube about 35 mm long. Basilar membrane,
Intro to Audition & Hearing
 Intro to Audition & Hearing Lecture 16 Chapter 9, part II Jonathan Pillow Sensation & Perception (PSY 345 / NEU 325) Fall 2017 1 Sine wave: one of the simplest kinds of sounds: sound for which pressure
Intro to Audition & Hearing Lecture 16 Chapter 9, part II Jonathan Pillow Sensation & Perception (PSY 345 / NEU 325) Fall 2017 1 Sine wave: one of the simplest kinds of sounds: sound for which pressure
Chapter 3: Anatomy and physiology of the sensory auditory mechanism
 Chapter 3: Anatomy and physiology of the sensory auditory mechanism Objectives (1) Anatomy of the inner ear Functions of the cochlear and vestibular systems Three compartments within the cochlea and membranes
Chapter 3: Anatomy and physiology of the sensory auditory mechanism Objectives (1) Anatomy of the inner ear Functions of the cochlear and vestibular systems Three compartments within the cochlea and membranes
Auditory Physiology Richard M. Costanzo, Ph.D.
 Auditory Physiology Richard M. Costanzo, Ph.D. OBJECTIVES After studying the material of this lecture, the student should be able to: 1. Describe the morphology and function of the following structures:
Auditory Physiology Richard M. Costanzo, Ph.D. OBJECTIVES After studying the material of this lecture, the student should be able to: 1. Describe the morphology and function of the following structures:
ENT 318 Artificial Organs Physiology of Ear
 ENT 318 Artificial Organs Physiology of Ear Lecturer: Ahmad Nasrul Norali The Ear The Ear Components of hearing mechanism - Outer Ear - Middle Ear - Inner Ear - Central Auditory Nervous System Major Divisions
ENT 318 Artificial Organs Physiology of Ear Lecturer: Ahmad Nasrul Norali The Ear The Ear Components of hearing mechanism - Outer Ear - Middle Ear - Inner Ear - Central Auditory Nervous System Major Divisions
Deafness and hearing impairment
 Auditory Physiology Deafness and hearing impairment About one in every 10 Americans has some degree of hearing loss. The great majority develop hearing loss as they age. Hearing impairment in very early
Auditory Physiology Deafness and hearing impairment About one in every 10 Americans has some degree of hearing loss. The great majority develop hearing loss as they age. Hearing impairment in very early
Chapter 11: Sound, The Auditory System, and Pitch Perception
 Chapter 11: Sound, The Auditory System, and Pitch Perception Overview of Questions What is it that makes sounds high pitched or low pitched? How do sound vibrations inside the ear lead to the perception
Chapter 11: Sound, The Auditory System, and Pitch Perception Overview of Questions What is it that makes sounds high pitched or low pitched? How do sound vibrations inside the ear lead to the perception
Required Slide. Session Objectives
 Auditory Physiology Required Slide Session Objectives Auditory System: At the end of this session, students will be able to: 1. Characterize the range of normal human hearing. 2. Understand the components
Auditory Physiology Required Slide Session Objectives Auditory System: At the end of this session, students will be able to: 1. Characterize the range of normal human hearing. 2. Understand the components
Cochlear anatomy, function and pathology I. Professor Dave Furness Keele University
 Cochlear anatomy, function and pathology I Professor Dave Furness Keele University d.n.furness@keele.ac.uk Aims and objectives of these lectures Introduction to gross anatomy of the cochlea Focus (1) on
Cochlear anatomy, function and pathology I Professor Dave Furness Keele University d.n.furness@keele.ac.uk Aims and objectives of these lectures Introduction to gross anatomy of the cochlea Focus (1) on
Improving the diagnostic power of otoacoustic emissions. Arturo Moleti Physics Department University of Roma Tor Vergata
 Improving the diagnostic power of otoacoustic emissions Arturo Moleti Physics Department University of Roma Tor Vergata The human ear Ear canal: resonant cavity Middle ear: impedance adapter and pressure
Improving the diagnostic power of otoacoustic emissions Arturo Moleti Physics Department University of Roma Tor Vergata The human ear Ear canal: resonant cavity Middle ear: impedance adapter and pressure
Acoustics Research Institute
 Austrian Academy of Sciences Acoustics Research Institute Modeling Modelingof ofauditory AuditoryPerception Perception Bernhard BernhardLaback Labackand andpiotr PiotrMajdak Majdak http://www.kfs.oeaw.ac.at
Austrian Academy of Sciences Acoustics Research Institute Modeling Modelingof ofauditory AuditoryPerception Perception Bernhard BernhardLaback Labackand andpiotr PiotrMajdak Majdak http://www.kfs.oeaw.ac.at
Can You Hear Me Now?
 An Introduction to the Mathematics of Hearing Department of Applied Mathematics University of Washington April 26, 2007 Some Questions How does hearing work? What are the important structures and mechanisms
An Introduction to the Mathematics of Hearing Department of Applied Mathematics University of Washington April 26, 2007 Some Questions How does hearing work? What are the important structures and mechanisms
MECHANISM OF HEARING
 MECHANISM OF HEARING Sound: Sound is a vibration that propagates as an audible wave of pressure, through a transmission medium such as gas, liquid or solid. Sound is produced from alternate compression
MECHANISM OF HEARING Sound: Sound is a vibration that propagates as an audible wave of pressure, through a transmission medium such as gas, liquid or solid. Sound is produced from alternate compression
Chapter 17, Part 2! The Special Senses! Hearing and Equilibrium!
 Chapter 17, Part 2! The Special Senses! Hearing and Equilibrium! SECTION 17-5! Equilibrium sensations originate within the inner ear, while hearing involves the detection and interpretation of sound waves!
Chapter 17, Part 2! The Special Senses! Hearing and Equilibrium! SECTION 17-5! Equilibrium sensations originate within the inner ear, while hearing involves the detection and interpretation of sound waves!
Chapter 17, Part 2! Chapter 17 Part 2 Special Senses! The Special Senses! Hearing and Equilibrium!
 Chapter 17, Part 2! The Special Senses! Hearing and Equilibrium! SECTION 17-5! Equilibrium sensations originate within the inner ear, while hearing involves the detection and interpretation of sound waves!
Chapter 17, Part 2! The Special Senses! Hearing and Equilibrium! SECTION 17-5! Equilibrium sensations originate within the inner ear, while hearing involves the detection and interpretation of sound waves!
Printable version - Hearing - OpenLearn - The Open University
 Skip to content Accessibility Sign in Contact Search the OU The Open University Study at the OU Research at the OU OU Community About the OU Hearing Printable page generated Saturday, 12 November 2011,
Skip to content Accessibility Sign in Contact Search the OU The Open University Study at the OU Research at the OU OU Community About the OU Hearing Printable page generated Saturday, 12 November 2011,
P T P V U V I. INTRODUCTION. II. MODEL FORMULATION A. Cochlear fluid dynamics.
 Integration of outer hair cell activity in a one-dimensional cochlear model Azaria Cohen and Miriam Furst a) School of Electrical Engineering, Faculty of Engineering, Tel-Aviv University, Tel-Aviv 69978,
Integration of outer hair cell activity in a one-dimensional cochlear model Azaria Cohen and Miriam Furst a) School of Electrical Engineering, Faculty of Engineering, Tel-Aviv University, Tel-Aviv 69978,
HEARING. Structure and Function
 HEARING Structure and Function Rory Attwood MBChB,FRCS Division of Otorhinolaryngology Faculty of Health Sciences Tygerberg Campus, University of Stellenbosch Analyse Function of auditory system Discriminate
HEARING Structure and Function Rory Attwood MBChB,FRCS Division of Otorhinolaryngology Faculty of Health Sciences Tygerberg Campus, University of Stellenbosch Analyse Function of auditory system Discriminate
Sound and its characteristics. The decibel scale. Structure and function of the ear. Békésy s theory. Molecular basis of hair cell function.
 Hearing Sound and its characteristics. The decibel scale. Structure and function of the ear. Békésy s theory. Molecular basis of hair cell function. 19/11/2014 Sound A type of longitudinal mass wave that
Hearing Sound and its characteristics. The decibel scale. Structure and function of the ear. Békésy s theory. Molecular basis of hair cell function. 19/11/2014 Sound A type of longitudinal mass wave that
Hearing: Physiology and Psychoacoustics
 9 Hearing: Physiology and Psychoacoustics Click Chapter to edit 9 Hearing: Master title Physiology style and Psychoacoustics The Function of Hearing What Is Sound? Basic Structure of the Mammalian Auditory
9 Hearing: Physiology and Psychoacoustics Click Chapter to edit 9 Hearing: Master title Physiology style and Psychoacoustics The Function of Hearing What Is Sound? Basic Structure of the Mammalian Auditory
Auditory System. Barb Rohrer (SEI )
 Auditory System Barb Rohrer (SEI614 2-5086) Sounds arise from mechanical vibration (creating zones of compression and rarefaction; which ripple outwards) Transmitted through gaseous, aqueous or solid medium
Auditory System Barb Rohrer (SEI614 2-5086) Sounds arise from mechanical vibration (creating zones of compression and rarefaction; which ripple outwards) Transmitted through gaseous, aqueous or solid medium
Auditory Physiology PSY 310 Greg Francis. Lecture 29. Hearing
 Auditory Physiology PSY 310 Greg Francis Lecture 29 A dangerous device. Hearing The sound stimulus is changes in pressure The simplest sounds vary in: Frequency: Hertz, cycles per second. How fast the
Auditory Physiology PSY 310 Greg Francis Lecture 29 A dangerous device. Hearing The sound stimulus is changes in pressure The simplest sounds vary in: Frequency: Hertz, cycles per second. How fast the
PSY 310: Sensory and Perceptual Processes 1
 Auditory Physiology PSY 310 Greg Francis Lecture 29 A dangerous device. Hearing The sound stimulus is changes in pressure The simplest sounds vary in: Frequency: Hertz, cycles per second. How fast the
Auditory Physiology PSY 310 Greg Francis Lecture 29 A dangerous device. Hearing The sound stimulus is changes in pressure The simplest sounds vary in: Frequency: Hertz, cycles per second. How fast the
Modelling the micromechanics of the cochlea in Femlab
 Modelling the micromechanics of the cochlea in Femlab R.R.J.J. van Doorn DCT 27.7 Traineeship report Coach(es): Supervisor: Prof. S.J. Elliott Prof. P. Gardonio Prof. H. Nijmeijer Technische Universiteit
Modelling the micromechanics of the cochlea in Femlab R.R.J.J. van Doorn DCT 27.7 Traineeship report Coach(es): Supervisor: Prof. S.J. Elliott Prof. P. Gardonio Prof. H. Nijmeijer Technische Universiteit
Systems Neuroscience Oct. 16, Auditory system. http:
 Systems Neuroscience Oct. 16, 2018 Auditory system http: www.ini.unizh.ch/~kiper/system_neurosci.html The physics of sound Measuring sound intensity We are sensitive to an enormous range of intensities,
Systems Neuroscience Oct. 16, 2018 Auditory system http: www.ini.unizh.ch/~kiper/system_neurosci.html The physics of sound Measuring sound intensity We are sensitive to an enormous range of intensities,
Processing of sounds in the inner ear
 Processing of sounds in the inner ear Sripriya Ramamoorthy Associate Professor, IIT Bombay WiSSAP 2018 Cochlea converts sound into electrical signals [Picture courtesy of Northwestern University] von Bekesy
Processing of sounds in the inner ear Sripriya Ramamoorthy Associate Professor, IIT Bombay WiSSAP 2018 Cochlea converts sound into electrical signals [Picture courtesy of Northwestern University] von Bekesy
HEARING AND PSYCHOACOUSTICS
 CHAPTER 2 HEARING AND PSYCHOACOUSTICS WITH LIDIA LEE I would like to lead off the specific audio discussions with a description of the audio receptor the ear. I believe it is always a good idea to understand
CHAPTER 2 HEARING AND PSYCHOACOUSTICS WITH LIDIA LEE I would like to lead off the specific audio discussions with a description of the audio receptor the ear. I believe it is always a good idea to understand
Hearing Sound. The Human Auditory System. The Outer Ear. Music 170: The Ear
 Hearing Sound Music 170: The Ear Tamara Smyth, trsmyth@ucsd.edu Department of Music, University of California, San Diego (UCSD) November 17, 2016 Sound interpretation in the auditory system is done by
Hearing Sound Music 170: The Ear Tamara Smyth, trsmyth@ucsd.edu Department of Music, University of California, San Diego (UCSD) November 17, 2016 Sound interpretation in the auditory system is done by
Music 170: The Ear. Tamara Smyth, Department of Music, University of California, San Diego (UCSD) November 17, 2016
 Music 170: The Ear Tamara Smyth, trsmyth@ucsd.edu Department of Music, University of California, San Diego (UCSD) November 17, 2016 1 Hearing Sound Sound interpretation in the auditory system is done by
Music 170: The Ear Tamara Smyth, trsmyth@ucsd.edu Department of Music, University of California, San Diego (UCSD) November 17, 2016 1 Hearing Sound Sound interpretation in the auditory system is done by
COM3502/4502/6502 SPEECH PROCESSING
 COM3502/4502/6502 SPEECH PROCESSING Lecture 4 Hearing COM3502/4502/6502 Speech Processing: Lecture 4, slide 1 The Speech Chain SPEAKER Ear LISTENER Feedback Link Vocal Muscles Ear Sound Waves Taken from:
COM3502/4502/6502 SPEECH PROCESSING Lecture 4 Hearing COM3502/4502/6502 Speech Processing: Lecture 4, slide 1 The Speech Chain SPEAKER Ear LISTENER Feedback Link Vocal Muscles Ear Sound Waves Taken from:
Unit VIII Problem 9 Physiology: Hearing
 Unit VIII Problem 9 Physiology: Hearing - We can hear a limited range of frequency between 20 Hz 20,000 Hz (human hearing acuity is between 1000 Hz 4000 Hz). - The ear is divided into 3 parts. Those are:
Unit VIII Problem 9 Physiology: Hearing - We can hear a limited range of frequency between 20 Hz 20,000 Hz (human hearing acuity is between 1000 Hz 4000 Hz). - The ear is divided into 3 parts. Those are:
A truly remarkable aspect of human hearing is the vast
 AUDITORY COMPRESSION AND HEARING LOSS Sid P. Bacon Psychoacoustics Laboratory, Department of Speech and Hearing Science, Arizona State University Tempe, Arizona 85287 A truly remarkable aspect of human
AUDITORY COMPRESSION AND HEARING LOSS Sid P. Bacon Psychoacoustics Laboratory, Department of Speech and Hearing Science, Arizona State University Tempe, Arizona 85287 A truly remarkable aspect of human
FIFTH INTERNATIONAL CONGRESS ON SOUND AND VIBRATION DECEMBER 15-18, 1997 ADELAIDE, SOUTH AUSTRALIA. Invited Paper LINEAR RESPONSE OF THE COCHLEA
 FIFTH INTERNATIONAL CONGRESS ON SOUND AND VIBRATION DECEMBER 15-18, 1997 ADELAIDE, SOUTH AUSTRALIA Invited Paper LINEAR RESPONSE OF THE COCHLEA David Alan Bies Visiting Research Fellow Department of Mechanical
FIFTH INTERNATIONAL CONGRESS ON SOUND AND VIBRATION DECEMBER 15-18, 1997 ADELAIDE, SOUTH AUSTRALIA Invited Paper LINEAR RESPONSE OF THE COCHLEA David Alan Bies Visiting Research Fellow Department of Mechanical
SPHSC 462 HEARING DEVELOPMENT. Overview Review of Hearing Science Introduction
 SPHSC 462 HEARING DEVELOPMENT Overview Review of Hearing Science Introduction 1 Overview of course and requirements Lecture/discussion; lecture notes on website http://faculty.washington.edu/lawerner/sphsc462/
SPHSC 462 HEARING DEVELOPMENT Overview Review of Hearing Science Introduction 1 Overview of course and requirements Lecture/discussion; lecture notes on website http://faculty.washington.edu/lawerner/sphsc462/
Nonlinear Cochlear Signal Processing
 Nonlinear Cochlear Signal Processing Jont B. Allen Florham Park, NJ March 13, 2001 Contents 1 Macromechanics 5 1.1 The early history of cochlear modeling...................... 6 1.2 The 1 model of the
Nonlinear Cochlear Signal Processing Jont B. Allen Florham Park, NJ March 13, 2001 Contents 1 Macromechanics 5 1.1 The early history of cochlear modeling...................... 6 1.2 The 1 model of the
Lecture 6 Hearing 1. Raghav Rajan Bio 354 Neurobiology 2 January 28th All lecture material from the following links unless otherwise mentioned:
 Lecture 6 Hearing 1 All lecture material from the following links unless otherwise mentioned: 1. http://wws.weizmann.ac.il/neurobiology/labs/ulanovsky/sites/neurobiology.labs.ulanovsky/files/uploads/purves_ch12_ch13_hearing
Lecture 6 Hearing 1 All lecture material from the following links unless otherwise mentioned: 1. http://wws.weizmann.ac.il/neurobiology/labs/ulanovsky/sites/neurobiology.labs.ulanovsky/files/uploads/purves_ch12_ch13_hearing
An active cochlear model showing sharp tuning and high sensitivity
 Hearing Research, 9 (1983) 123-13 Elsevier Biomedical Press 123 An active cochlear model showing sharp tuning and high sensitivity Stephen T. Neely * and D.O. Kim Box 811, Washington Unitlersit}', St.
Hearing Research, 9 (1983) 123-13 Elsevier Biomedical Press 123 An active cochlear model showing sharp tuning and high sensitivity Stephen T. Neely * and D.O. Kim Box 811, Washington Unitlersit}', St.
SPECIAL SENSES: THE AUDITORY SYSTEM
 SPECIAL SENSES: THE AUDITORY SYSTEM REVISION OF PHYSICS: WAVES A wave is an oscillation of power, sound waves have two main characteristics: amplitude, which is the maximum displacement or the power of
SPECIAL SENSES: THE AUDITORY SYSTEM REVISION OF PHYSICS: WAVES A wave is an oscillation of power, sound waves have two main characteristics: amplitude, which is the maximum displacement or the power of
Receptors / physiology
 Hearing: physiology Receptors / physiology Energy transduction First goal of a sensory/perceptual system? Transduce environmental energy into neural energy (or energy that can be interpreted by perceptual
Hearing: physiology Receptors / physiology Energy transduction First goal of a sensory/perceptual system? Transduce environmental energy into neural energy (or energy that can be interpreted by perceptual
Representation of sound in the auditory nerve
 Representation of sound in the auditory nerve Eric D. Young Department of Biomedical Engineering Johns Hopkins University Young, ED. Neural representation of spectral and temporal information in speech.
Representation of sound in the auditory nerve Eric D. Young Department of Biomedical Engineering Johns Hopkins University Young, ED. Neural representation of spectral and temporal information in speech.
HST 721 Lecture 4: Mechanics, electromotility and the cochlear amplifier
 HST 721 Lecture 4: Mechanics, electromotility and the cochlear amplifier 1 Cochlear Mechanics: Measures of Basilar Membrane Motion 2 Cochlear Mechanics: Measures of Basilar Membrane Motion Bekesy s experiments
HST 721 Lecture 4: Mechanics, electromotility and the cochlear amplifier 1 Cochlear Mechanics: Measures of Basilar Membrane Motion 2 Cochlear Mechanics: Measures of Basilar Membrane Motion Bekesy s experiments
Anatomy and Physiology of Hearing
 Anatomy and Physiology of Hearing The Human Ear Temporal Bone Found on each side of the skull and contains the organs for hearing and balance Divided into four major portions: - squamous - mastoid - tympanic
Anatomy and Physiology of Hearing The Human Ear Temporal Bone Found on each side of the skull and contains the organs for hearing and balance Divided into four major portions: - squamous - mastoid - tympanic
Auditory Periphery! external middle inner. stapes movement initiates a pressure wave in cochlear fluid
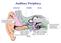 Auditory Periphery! external middle inner sound causes air pressure to increase at eardrum stapes movement initiates a pressure wave in cochlear fluid VIIIth nerve conveys neural signal to cochlear nucleus
Auditory Periphery! external middle inner sound causes air pressure to increase at eardrum stapes movement initiates a pressure wave in cochlear fluid VIIIth nerve conveys neural signal to cochlear nucleus
The frequency analysis of the cochlea a review of Nobili et al (1998) and Ruggero et al (1992)
 The frequency analysis of the cochlea a review of Nobili et al (1998) and Ruggero et al (1992) by Pedro da Fonseca (pedrofon@mail.telepac.pt) Neuroscience course Presented in 17.12.99 to professor STEPHEN
The frequency analysis of the cochlea a review of Nobili et al (1998) and Ruggero et al (1992) by Pedro da Fonseca (pedrofon@mail.telepac.pt) Neuroscience course Presented in 17.12.99 to professor STEPHEN
Comparing in vitro, in situ, and in vivo experimental data in a three-dimensional model of mammalian cochlear mechanics
 Proc. Natl. Acad. Sci. USA Vol. 96, pp. 3676 3681, March 1999 Biophysics Comparing in vitro, in situ, and in vivo experimental data in a three-dimensional model of mammalian cochlear mechanics PAUL J.
Proc. Natl. Acad. Sci. USA Vol. 96, pp. 3676 3681, March 1999 Biophysics Comparing in vitro, in situ, and in vivo experimental data in a three-dimensional model of mammalian cochlear mechanics PAUL J.
College of Medicine Dept. of Medical physics Physics of ear and hearing /CH
 College of Medicine Dept. of Medical physics Physics of ear and hearing /CH 13 2017-2018 ***************************************************************** o Introduction : The ear is the organ that detects
College of Medicine Dept. of Medical physics Physics of ear and hearing /CH 13 2017-2018 ***************************************************************** o Introduction : The ear is the organ that detects
Lecture 3: Perception
 ELEN E4896 MUSIC SIGNAL PROCESSING Lecture 3: Perception 1. Ear Physiology 2. Auditory Psychophysics 3. Pitch Perception 4. Music Perception Dan Ellis Dept. Electrical Engineering, Columbia University
ELEN E4896 MUSIC SIGNAL PROCESSING Lecture 3: Perception 1. Ear Physiology 2. Auditory Psychophysics 3. Pitch Perception 4. Music Perception Dan Ellis Dept. Electrical Engineering, Columbia University
Hearing and Balance 1
 Hearing and Balance 1 Slide 3 Sound is produced by vibration of an object which produces alternating waves of pressure and rarefaction, for example this tuning fork. Slide 4 Two characteristics of sound
Hearing and Balance 1 Slide 3 Sound is produced by vibration of an object which produces alternating waves of pressure and rarefaction, for example this tuning fork. Slide 4 Two characteristics of sound
Acoustics, signals & systems for audiology. Psychoacoustics of hearing impairment
 Acoustics, signals & systems for audiology Psychoacoustics of hearing impairment Three main types of hearing impairment Conductive Sound is not properly transmitted from the outer to the inner ear Sensorineural
Acoustics, signals & systems for audiology Psychoacoustics of hearing impairment Three main types of hearing impairment Conductive Sound is not properly transmitted from the outer to the inner ear Sensorineural
The Ear. The ear can be divided into three major parts: the outer ear, the middle ear and the inner ear.
 The Ear The ear can be divided into three major parts: the outer ear, the middle ear and the inner ear. The Ear There are three components of the outer ear: Pinna: the fleshy outer part of the ear which
The Ear The ear can be divided into three major parts: the outer ear, the middle ear and the inner ear. The Ear There are three components of the outer ear: Pinna: the fleshy outer part of the ear which
HCS 7367 Speech Perception
 Long-term spectrum of speech HCS 7367 Speech Perception Connected speech Absolute threshold Males Dr. Peter Assmann Fall 212 Females Long-term spectrum of speech Vowels Males Females 2) Absolute threshold
Long-term spectrum of speech HCS 7367 Speech Perception Connected speech Absolute threshold Males Dr. Peter Assmann Fall 212 Females Long-term spectrum of speech Vowels Males Females 2) Absolute threshold
Auditory Physiology PSY 310 Greg Francis. Lecture 30. Organ of Corti
 Auditory Physiology PSY 310 Greg Francis Lecture 30 Waves, waves, waves. Organ of Corti Tectorial membrane Sits on top Inner hair cells Outer hair cells The microphone for the brain 1 Hearing Perceptually,
Auditory Physiology PSY 310 Greg Francis Lecture 30 Waves, waves, waves. Organ of Corti Tectorial membrane Sits on top Inner hair cells Outer hair cells The microphone for the brain 1 Hearing Perceptually,
! Can hear whistle? ! Where are we on course map? ! What we did in lab last week. ! Psychoacoustics
 2/14/18 Can hear whistle? Lecture 5 Psychoacoustics Based on slides 2009--2018 DeHon, Koditschek Additional Material 2014 Farmer 1 2 There are sounds we cannot hear Depends on frequency Where are we on
2/14/18 Can hear whistle? Lecture 5 Psychoacoustics Based on slides 2009--2018 DeHon, Koditschek Additional Material 2014 Farmer 1 2 There are sounds we cannot hear Depends on frequency Where are we on
What is the effect on the hair cell if the stereocilia are bent away from the kinocilium?
 CASE 44 A 53-year-old man presents to his primary care physician with complaints of feeling like the room is spinning, dizziness, decreased hearing, ringing in the ears, and fullness in both ears. He states
CASE 44 A 53-year-old man presents to his primary care physician with complaints of feeling like the room is spinning, dizziness, decreased hearing, ringing in the ears, and fullness in both ears. He states
Cochlear anatomy, function and pathology II. Professor Dave Furness Keele University
 Cochlear anatomy, function and pathology II Professor Dave Furness Keele University d.n.furness@keele.ac.uk Aims and objectives of this lecture Focus (2) on the biophysics of the cochlea, the dual roles
Cochlear anatomy, function and pathology II Professor Dave Furness Keele University d.n.furness@keele.ac.uk Aims and objectives of this lecture Focus (2) on the biophysics of the cochlea, the dual roles
Spectrograms (revisited)
 Spectrograms (revisited) We begin the lecture by reviewing the units of spectrograms, which I had only glossed over when I covered spectrograms at the end of lecture 19. We then relate the blocks of a
Spectrograms (revisited) We begin the lecture by reviewing the units of spectrograms, which I had only glossed over when I covered spectrograms at the end of lecture 19. We then relate the blocks of a
Chapter Fourteen. The Hearing Mechanism. 1. Introduction.
 Chapter Fourteen The Hearing Mechanism 1. Introduction. 2. Hearing. 3. The Ear. 4. The External Ear. 5. The Inner Ear. 6. Frequency Discrimination. 7. The Organ of Corti. 8. Tests and Exrecises. 9. References.
Chapter Fourteen The Hearing Mechanism 1. Introduction. 2. Hearing. 3. The Ear. 4. The External Ear. 5. The Inner Ear. 6. Frequency Discrimination. 7. The Organ of Corti. 8. Tests and Exrecises. 9. References.
to vibrate the fluid. The ossicles amplify the pressure. The surface area of the oval window is
 Page 1 of 6 Question 1: How is the conduction of sound to the cochlea facilitated by the ossicles of the middle ear? Answer: Sound waves traveling through air move the tympanic membrane, which, in turn,
Page 1 of 6 Question 1: How is the conduction of sound to the cochlea facilitated by the ossicles of the middle ear? Answer: Sound waves traveling through air move the tympanic membrane, which, in turn,
Hearing. By: Jimmy, Dana, and Karissa
 Hearing By: Jimmy, Dana, and Karissa Anatomy - The ear is divided up into three parts - Sound enters in through the outer ear and passes into the middle where the vibrations are received and sent to the
Hearing By: Jimmy, Dana, and Karissa Anatomy - The ear is divided up into three parts - Sound enters in through the outer ear and passes into the middle where the vibrations are received and sent to the
Hearing. istockphoto/thinkstock
 Hearing istockphoto/thinkstock Audition The sense or act of hearing The Stimulus Input: Sound Waves Sound waves are composed of changes in air pressure unfolding over time. Acoustical transduction: Conversion
Hearing istockphoto/thinkstock Audition The sense or act of hearing The Stimulus Input: Sound Waves Sound waves are composed of changes in air pressure unfolding over time. Acoustical transduction: Conversion
THE EAR AND HEARING Be sure you have read and understand Chapter 16 before beginning this lab. INTRODUCTION: hair cells outer ear tympanic membrane
 BIOLOGY 211: HUMAN ANATOMY & PHYSIOLOGY ****************************************************************************************************** THE EAR AND HEARING ******************************************************************************************************
BIOLOGY 211: HUMAN ANATOMY & PHYSIOLOGY ****************************************************************************************************** THE EAR AND HEARING ******************************************************************************************************
Signals, systems, acoustics and the ear. Week 5. The peripheral auditory system: The ear as a signal processor
 Signals, systems, acoustics and the ear Week 5 The peripheral auditory system: The ear as a signal processor Think of this set of organs 2 as a collection of systems, transforming sounds to be sent to
Signals, systems, acoustics and the ear Week 5 The peripheral auditory system: The ear as a signal processor Think of this set of organs 2 as a collection of systems, transforming sounds to be sent to
A Bidirectional Analog VLSI Cochlear Model
 A Bidirectional Analog VLSI Cochlear Model Lloyd Watts Richard F. Lyon 1 Carver Mead Department of Computer Science California Institute of Technology Pasadena, CA USA 91125 Abstract A novel circuit is
A Bidirectional Analog VLSI Cochlear Model Lloyd Watts Richard F. Lyon 1 Carver Mead Department of Computer Science California Institute of Technology Pasadena, CA USA 91125 Abstract A novel circuit is
The Structure and Function of the Auditory Nerve
 The Structure and Function of the Auditory Nerve Brad May Structure and Function of the Auditory and Vestibular Systems (BME 580.626) September 21, 2010 1 Objectives Anatomy Basic response patterns Frequency
The Structure and Function of the Auditory Nerve Brad May Structure and Function of the Auditory and Vestibular Systems (BME 580.626) September 21, 2010 1 Objectives Anatomy Basic response patterns Frequency
PSY 215 Lecture 10 Topic: Hearing Chapter 7, pages
 PSY 215 Lecture 10 Topic: Hearing Chapter 7, pages 189-197 Corrections: NTC 09-1, page 3, the Superior Colliculus is in the midbrain (Mesencephalon). Announcements: Movie next Monday: Case of the frozen
PSY 215 Lecture 10 Topic: Hearing Chapter 7, pages 189-197 Corrections: NTC 09-1, page 3, the Superior Colliculus is in the midbrain (Mesencephalon). Announcements: Movie next Monday: Case of the frozen
external middle inner
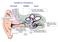 Auditory Periphery external middle inner 3. movement of stapes initiates a pressure wave in cochlear fluid. 1. sound causes air pressure to increase at eardrum 5. auditory nerve conveys neural signal to
Auditory Periphery external middle inner 3. movement of stapes initiates a pressure wave in cochlear fluid. 1. sound causes air pressure to increase at eardrum 5. auditory nerve conveys neural signal to
Detailed Simulation of the Cochlea: Recent Progress Using Large Shared Memory Parallel Computers
 Detailed Simulation of the Cochlea: Recent Progress Using Large Shared Memory Parallel Computers E. Givelberg Department of Mathematics, University of Michigan, Ann Arbor, MI givelbrg@cims.nyu.edu M. Rajan
Detailed Simulation of the Cochlea: Recent Progress Using Large Shared Memory Parallel Computers E. Givelberg Department of Mathematics, University of Michigan, Ann Arbor, MI givelbrg@cims.nyu.edu M. Rajan
Sound. Audition. Physics of Sound. Properties of sound. Perception of sound works the same way as light.
 Sound Audition Perception of sound works the same way as light. Have receptors to convert a physical stimulus to action potentials Action potentials are organized in brain structures You apply some meaning
Sound Audition Perception of sound works the same way as light. Have receptors to convert a physical stimulus to action potentials Action potentials are organized in brain structures You apply some meaning
Audition. Sound. Physics of Sound. Perception of sound works the same way as light.
 Audition Sound Perception of sound works the same way as light. Have receptors to convert a physical stimulus to action potentials Action potentials are organized in brain structures You apply some meaning
Audition Sound Perception of sound works the same way as light. Have receptors to convert a physical stimulus to action potentials Action potentials are organized in brain structures You apply some meaning
What does it mean to analyze the frequency components of a sound? A spectrogram such as that shown here is the usual display of frequency components
 1 2 3 4 What does it mean to analyze the frequency components of a sound? A spectrogram such as that shown here is the usual display of frequency components as a function of time here during the production
1 2 3 4 What does it mean to analyze the frequency components of a sound? A spectrogram such as that shown here is the usual display of frequency components as a function of time here during the production
Before we talk about the auditory system we will talk about the sound and waves
 The Auditory System PHYSIO: #3 DR.LOAI ZAGOUL 24/3/2014 Refer to the slides for some photos. Before we talk about the auditory system we will talk about the sound and waves All waves have basic characteristics:
The Auditory System PHYSIO: #3 DR.LOAI ZAGOUL 24/3/2014 Refer to the slides for some photos. Before we talk about the auditory system we will talk about the sound and waves All waves have basic characteristics:
Ear. Utricle & saccule in the vestibule Connected to each other and to the endolymphatic sac by a utriculosaccular duct
 Rahaf Jreisat *You don t have to go back to the slides. Ear Inner Ear Membranous Labyrinth It is a reflection of bony labyrinth but inside. Membranous labyrinth = set of membranous tubes containing sensory
Rahaf Jreisat *You don t have to go back to the slides. Ear Inner Ear Membranous Labyrinth It is a reflection of bony labyrinth but inside. Membranous labyrinth = set of membranous tubes containing sensory
A cochlear AGC model, proposing a new type of cochlear non-linearity
 TEL-AVIV UNIVERSITY The Iby and Aladar Fleischman faculty of engineering The Zandman-Slaner school of Graduate studies A cochlear AGC model, proposing a new type of cochlear non-linearity A thesis submitted
TEL-AVIV UNIVERSITY The Iby and Aladar Fleischman faculty of engineering The Zandman-Slaner school of Graduate studies A cochlear AGC model, proposing a new type of cochlear non-linearity A thesis submitted
Human Acoustic Processing
 Human Acoustic Processing Sound and Light The Ear Cochlea Auditory Pathway Speech Spectrogram Vocal Cords Formant Frequencies Time Warping Hidden Markov Models Signal, Time and Brain Process of temporal
Human Acoustic Processing Sound and Light The Ear Cochlea Auditory Pathway Speech Spectrogram Vocal Cords Formant Frequencies Time Warping Hidden Markov Models Signal, Time and Brain Process of temporal
A Brief History of Auditory Models
 A Brief History of Auditory Models Leonardo C. Araújo 1, Tairone N. Magalhaes 1, Damares P. M. Souza 1, Hani C. Yehia 1, Maurício A. Loureiro 1 1 CEFALA - Center for Research on Speech, Acoustics, Language
A Brief History of Auditory Models Leonardo C. Araújo 1, Tairone N. Magalhaes 1, Damares P. M. Souza 1, Hani C. Yehia 1, Maurício A. Loureiro 1 1 CEFALA - Center for Research on Speech, Acoustics, Language
Sound Waves. Sensation and Perception. Sound Waves. Sound Waves. Sound Waves
 Sensation and Perception Part 3 - Hearing Sound comes from pressure waves in a medium (e.g., solid, liquid, gas). Although we usually hear sounds in air, as long as the medium is there to transmit the
Sensation and Perception Part 3 - Hearing Sound comes from pressure waves in a medium (e.g., solid, liquid, gas). Although we usually hear sounds in air, as long as the medium is there to transmit the
Sound and the auditory system
 978--521-68889-5 - Auditory Perception: An Analysis and Synthesis, Third Edition 1 Sound and the auditory system This chapter provides a brief introduction to the physical nature of sound, the manner in
978--521-68889-5 - Auditory Perception: An Analysis and Synthesis, Third Edition 1 Sound and the auditory system This chapter provides a brief introduction to the physical nature of sound, the manner in
Sound and Hearing. Decibels. Frequency Coding & Localization 1. Everything is vibration. The universe is made of waves.
 Frequency Coding & Localization 1 Sound and Hearing Everything is vibration The universe is made of waves db = 2log(P1/Po) P1 = amplitude of the sound wave Po = reference pressure =.2 dynes/cm 2 Decibels
Frequency Coding & Localization 1 Sound and Hearing Everything is vibration The universe is made of waves db = 2log(P1/Po) P1 = amplitude of the sound wave Po = reference pressure =.2 dynes/cm 2 Decibels
AUDITORY APPARATUS. Mr. P Mazengenya. Tel 72204
 AUDITORY APPARATUS Mr. P Mazengenya Tel 72204 Describe the anatomical features of the external ear Describe the tympanic membrane (ear drum) Describe the walls of the middle ear Outline the structures
AUDITORY APPARATUS Mr. P Mazengenya Tel 72204 Describe the anatomical features of the external ear Describe the tympanic membrane (ear drum) Describe the walls of the middle ear Outline the structures
BCS 221: Auditory Perception BCS 521 & PSY 221
 BCS 221: Auditory Perception BCS 521 & PSY 221 Time: MW 10:25 11:40 AM Recitation: F 10:25 11:25 AM Room: Hutchinson 473 Lecturer: Dr. Kevin Davis Office: 303E Meliora Hall Office hours: M 1 3 PM kevin_davis@urmc.rochester.edu
BCS 221: Auditory Perception BCS 521 & PSY 221 Time: MW 10:25 11:40 AM Recitation: F 10:25 11:25 AM Room: Hutchinson 473 Lecturer: Dr. Kevin Davis Office: 303E Meliora Hall Office hours: M 1 3 PM kevin_davis@urmc.rochester.edu
The cochlea: auditory sense. The cochlea: auditory sense
 Inner ear apparatus 1- Vestibule macula and sacculus sensing acceleration of the head and direction of gravity 2- Semicircular canals mainly for sensing direction of rotation of the head 1 3- cochlea in
Inner ear apparatus 1- Vestibule macula and sacculus sensing acceleration of the head and direction of gravity 2- Semicircular canals mainly for sensing direction of rotation of the head 1 3- cochlea in
EMANATIONS FROM RESIDUUM OSCILLATIONS IN HUMAN AUDITORY SYSTEM
 EMANATIONS FROM RESIDUUM OSCILLATIONS IN HUMAN AUDITORY SYSTEM V.S. Balaji, N.R.Raajan, S. Rakesh Kumar, Har Narayan Upadhyay School of Electrical & Electronics Engineering, SASTRA University Thanjavur,
EMANATIONS FROM RESIDUUM OSCILLATIONS IN HUMAN AUDITORY SYSTEM V.S. Balaji, N.R.Raajan, S. Rakesh Kumar, Har Narayan Upadhyay School of Electrical & Electronics Engineering, SASTRA University Thanjavur,
Hearing Lectures. Acoustics of Speech and Hearing. Auditory Lighthouse. Facts about Timbre. Analysis of Complex Sounds
 Hearing Lectures Acoustics of Speech and Hearing Week 2-10 Hearing 3: Auditory Filtering 1. Loudness of sinusoids mainly (see Web tutorial for more) 2. Pitch of sinusoids mainly (see Web tutorial for more)
Hearing Lectures Acoustics of Speech and Hearing Week 2-10 Hearing 3: Auditory Filtering 1. Loudness of sinusoids mainly (see Web tutorial for more) 2. Pitch of sinusoids mainly (see Web tutorial for more)
Hearing. Figure 1. The human ear (from Kessel and Kardon, 1979)
 Hearing The nervous system s cognitive response to sound stimuli is known as psychoacoustics: it is partly acoustics and partly psychology. Hearing is a feature resulting from our physiology that we tend
Hearing The nervous system s cognitive response to sound stimuli is known as psychoacoustics: it is partly acoustics and partly psychology. Hearing is a feature resulting from our physiology that we tend
THE COCHLEA AND AUDITORY PATHWAY
 Dental Neuroanatomy Suzanne S. Stensaas, PhD February 23, 2012 Reading: Waxman, Chapter 16, Review pictures in a Histology book Computer Resources: http://www.cochlea.org/ - Promenade around the Cochlea
Dental Neuroanatomy Suzanne S. Stensaas, PhD February 23, 2012 Reading: Waxman, Chapter 16, Review pictures in a Histology book Computer Resources: http://www.cochlea.org/ - Promenade around the Cochlea
9.01 Introduction to Neuroscience Fall 2007
 MIT OpenCourseWare http://ocw.mit.edu 9.01 Introduction to Neuroscience Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 9.01 Recitation (R02)
MIT OpenCourseWare http://ocw.mit.edu 9.01 Introduction to Neuroscience Fall 2007 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 9.01 Recitation (R02)
ID# Final Exam PS325, Fall 1997
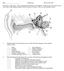 ID# Final Exam PS325, Fall 1997 Good luck on this exam. Answer each question carefully and completely. Keep your eyes foveated on your own exam, as the Skidmore Honor Code is in effect (as always). Have
ID# Final Exam PS325, Fall 1997 Good luck on this exam. Answer each question carefully and completely. Keep your eyes foveated on your own exam, as the Skidmore Honor Code is in effect (as always). Have
Computational Models of Mammalian Hearing:
 Computational Models of Mammalian Hearing: Frank Netter and his Ciba paintings An Auditory Image Approach Dick Lyon For Tom Dean s Cortex Class Stanford, April 14, 2010 Breschet 1836, Testut 1897 167 years
Computational Models of Mammalian Hearing: Frank Netter and his Ciba paintings An Auditory Image Approach Dick Lyon For Tom Dean s Cortex Class Stanford, April 14, 2010 Breschet 1836, Testut 1897 167 years
A&P 1. Ear, Hearing & Equilibrium Lab. Basic Concepts. These notes follow Carl s Talk at the beginning of lab
 A&P 1 Ear, Hearing & Equilibrium Lab Basic Concepts These notes follow Carl s Talk at the beginning of lab In this "Lab Exercise Guide", we will be looking at the basics of hearing and equilibrium. NOTE:
A&P 1 Ear, Hearing & Equilibrium Lab Basic Concepts These notes follow Carl s Talk at the beginning of lab In this "Lab Exercise Guide", we will be looking at the basics of hearing and equilibrium. NOTE:
Educational Module Tympanometry. Germany D Germering
 Educational Module anometry PATH medical Germany D-82110 Germering Our educational modules 1 are made for providing information on how the hearing organ works and which test procedures are used to test
Educational Module anometry PATH medical Germany D-82110 Germering Our educational modules 1 are made for providing information on how the hearing organ works and which test procedures are used to test
Healthy Organ of Corti. Loss of OHCs. How to use and interpret the TEN(HL) test for diagnosis of Dead Regions in the cochlea
 'How we do it' Healthy Organ of Corti How to use and interpret the TEN(HL) test for diagnosis of s in the cochlea Karolina Kluk¹ Brian C.J. Moore² Mouse IHCs OHCs ¹ Audiology and Deafness Research Group,
'How we do it' Healthy Organ of Corti How to use and interpret the TEN(HL) test for diagnosis of s in the cochlea Karolina Kluk¹ Brian C.J. Moore² Mouse IHCs OHCs ¹ Audiology and Deafness Research Group,
AUDL GS08 and GAV1: 2013 Final exam page 1/13. You must complete all sections. Label all graphs. Show your work!
 AUDL GS08 and GAV1: 2013 Final exam page 1/13 You must complete all sections. Label all graphs. Show your work! Section A: Short questions concerning Signals & Systems A1. Give the sound pressure levels
AUDL GS08 and GAV1: 2013 Final exam page 1/13 You must complete all sections. Label all graphs. Show your work! Section A: Short questions concerning Signals & Systems A1. Give the sound pressure levels
Chapter 7. Audition, the Body Senses, and the Chemical Senses. Copyright Allyn & Bacon 2004
 Chapter 7 Audition, the Body Senses, and the Chemical Senses This multimedia product and its contents are protected under copyright law. The following are prohibited by law: any public performance or display,
Chapter 7 Audition, the Body Senses, and the Chemical Senses This multimedia product and its contents are protected under copyright law. The following are prohibited by law: any public performance or display,
Hearing. and other senses
 Hearing and other senses Sound Sound: sensed variations in air pressure Frequency: number of peaks that pass a point per second (Hz) Pitch 2 Some Sound and Hearing Links Useful (and moderately entertaining)
Hearing and other senses Sound Sound: sensed variations in air pressure Frequency: number of peaks that pass a point per second (Hz) Pitch 2 Some Sound and Hearing Links Useful (and moderately entertaining)
Chapter 15 Hearing & Equilibrium
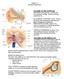 Chapter 15 Hearing & Equilibrium ANATOMY OF THE OUTER EAR EAR PINNA is the outer ear it is thin skin covering elastic cartilage. It directs incoming sound waves to the EXTERNAL AUDITORY CANAL, which is
Chapter 15 Hearing & Equilibrium ANATOMY OF THE OUTER EAR EAR PINNA is the outer ear it is thin skin covering elastic cartilage. It directs incoming sound waves to the EXTERNAL AUDITORY CANAL, which is
PSY 214 Lecture 16 (11/09/2011) (Sound, auditory system & pitch perception) Dr. Achtman PSY 214
 PSY 214 Lecture 16 Topic: Sound, auditory system, & pitch perception Chapter 11, pages 268-288 Corrections: None needed Announcements: At the beginning of class, we went over some demos from the virtual
PSY 214 Lecture 16 Topic: Sound, auditory system, & pitch perception Chapter 11, pages 268-288 Corrections: None needed Announcements: At the beginning of class, we went over some demos from the virtual
Presentation On SENSATION. Prof- Mrs.Kuldeep Kaur
 Presentation On SENSATION Prof- Mrs.Kuldeep Kaur INTRODUCTION:- Sensation is a specialty area within Psychology that works at understanding how are senses work and how we perceive stimuli in the environment.
Presentation On SENSATION Prof- Mrs.Kuldeep Kaur INTRODUCTION:- Sensation is a specialty area within Psychology that works at understanding how are senses work and how we perceive stimuli in the environment.
